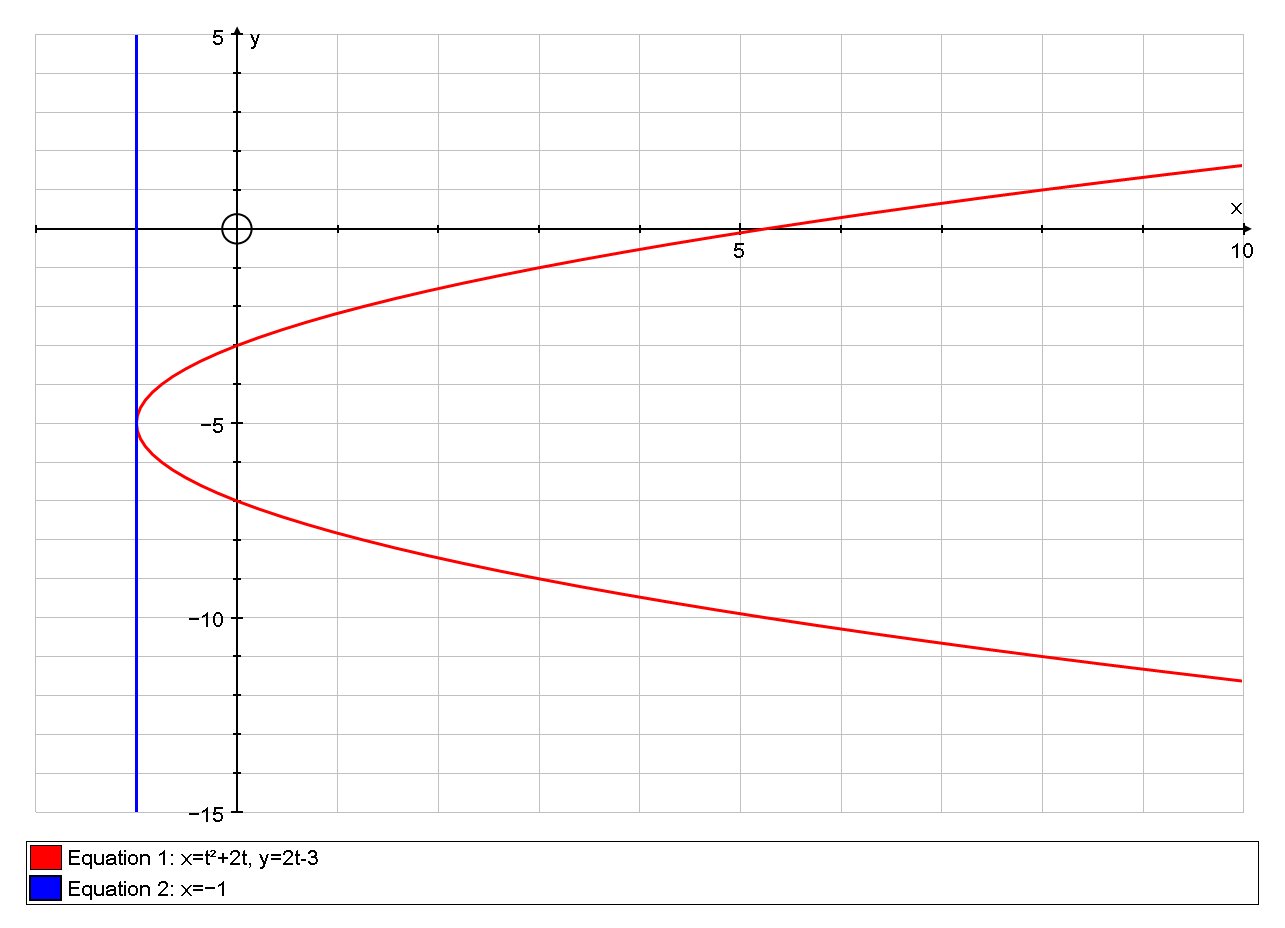
What is the slope of #f(t) = (t^2+2t,2t-3)# at #t =-1#?

Question

1292 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-11-10T02:53:05

The slope of #f(t)# is infinite when #t=-1# (ie the tangent is vertical).

We have # f(t)=(x(t), y(t)) # Where #x(t)=t^2+2t#, #y(t)=2t-3#

The by the chain rule, # dy/dx = dy/dt * dt/dx = (dy/dt) / (dx/dt) #

# x(t)=t^2+2t => dx/dt=2t+2 #
# y(t)=2t-3 => dy/dt = 2 #

So,

# dy/dx = 2 / (2t+2) #
# :. dy/dx = 1 / (t+1) #

When # t=-1 => dy/dx = 1/0 = oo #, so the slope of #f(t)# is infinite when #t=-1# (ie the tangent is vertical).

This can be visualised by looking at the graph of #f(t)#

enter image source here