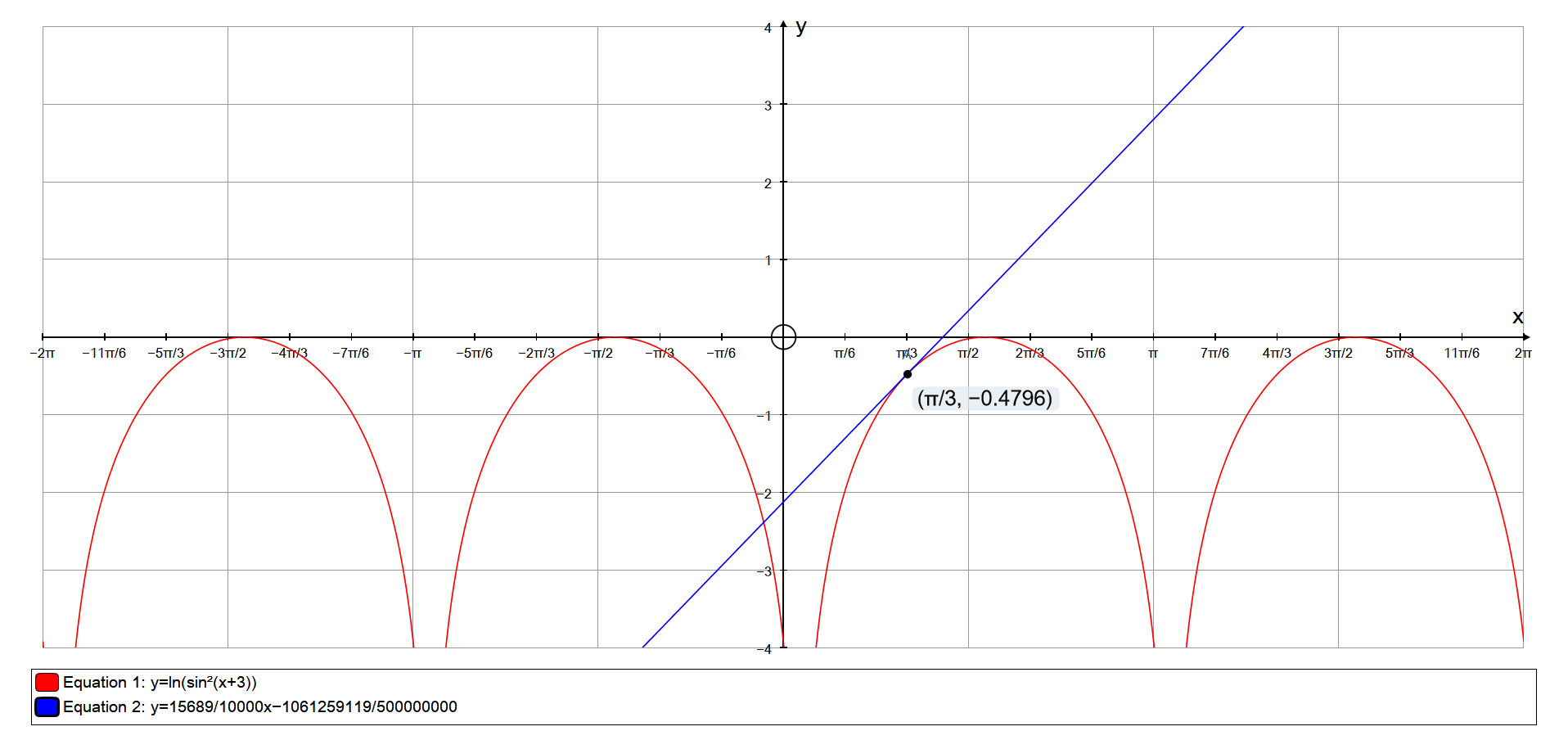
What is the slope of the line tangent to the graph of the function #f(x)=ln(sin^2(x+3))# at the point where #x=pi/3#?
1 Answer
Mar 14, 2018
See below.
Explanation:
If:
Using this definition with given function:
Differentiating implicitly:
Dividing by
Cancelling common factors:
We now have the derivative and will therefore be able to calculate the gradient at
Plugging in this value:
This is the approximate equation of the line:
GRAPH: