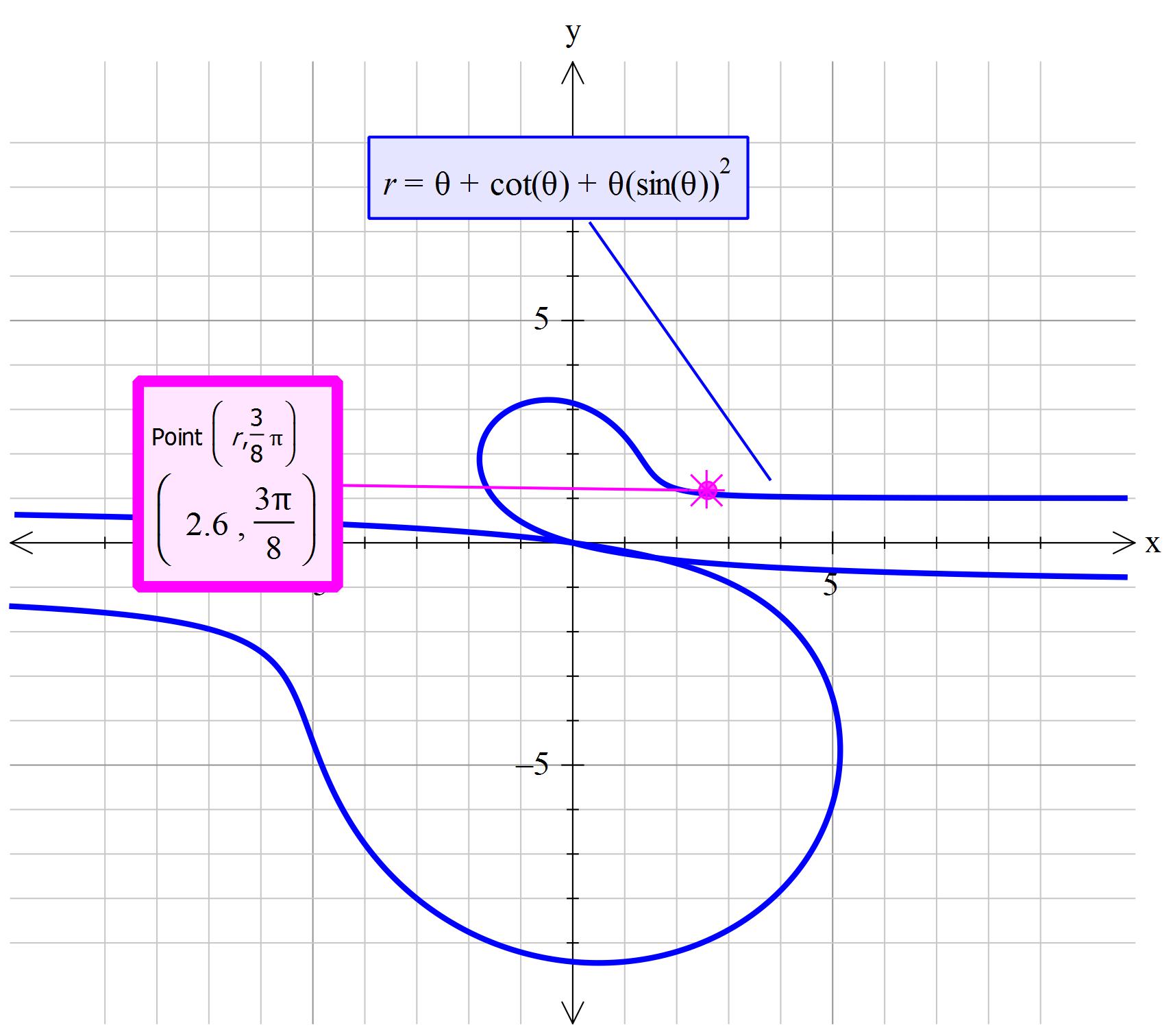
What is the slope of the polar curve f(theta) = theta + cottheta+thetasin^2theta at theta = (3pi)/8?
2 Answers
Jul 5, 2016
Explanation:
- The slope of any curve/function at a certain point is always the function's first derivative.
Hence, the slope off(theta)=f'(theta) f'(theta)=1-csc^2theta+theta*2sintheta*costheta+sin^2theta
=1-csc^2theta+thetasin2theta+sin^2theta - Therefore, the slope at
theta=(3pi)/8 is
f'((3pi)/8)=1-csc^2((3pi)/8)+(3pi)/8sin2((3pi)/8)+sin^2((3pi)/8)
=1-1.17+0.83+0.85
=1.51
Jul 5, 2016
Added graph
Explanation:
The graphing package I am using must have a slight error in the coding as the point does not sit exactly on the plotted line.
However; the uploaded image should give you a rough guide.