Question

What is the slope of the polar curve `f(theta) = -theta + sectheta - costheta` at `theta = (5pi)/4`?

Answer 1

The slope, `m ~~ = -5.12`

Explanation:

Given: `r(theta) = sec(theta) - cos(theta) - theta" [1]"`

The reference Tangents to a polar curve gives us the following equation for `dy/dx`:

`dy/dx = (r'(theta)sin(theta) + r(theta)cos(theta))/(r'(theta)cos(theta) - r(theta)sin(theta))" [2]"`

Compute the first derivative of equation [1]:

`r'(theta) = sin(theta) + tan(theta) sec(theta) - 1" [3]"`

Substitute equation [1] and equation [3] into equation [2]:

`dy/dx = ((sin(theta) + tan(theta) sec(theta) - 1)sin(theta) + (sec(theta) - cos(theta) - theta)cos(theta))/((sin(theta) + tan(theta) sec(theta) - 1)cos(theta) - (sec(theta) - cos(theta) - theta)sin(theta))" [4]"`

Evaluate equation [4] at `theta = (5pi)/4`:

`m ~~ = -5.12`
Here is the equation of the tangent line:

`y =-5.12(x -3.2768) +3.2768`

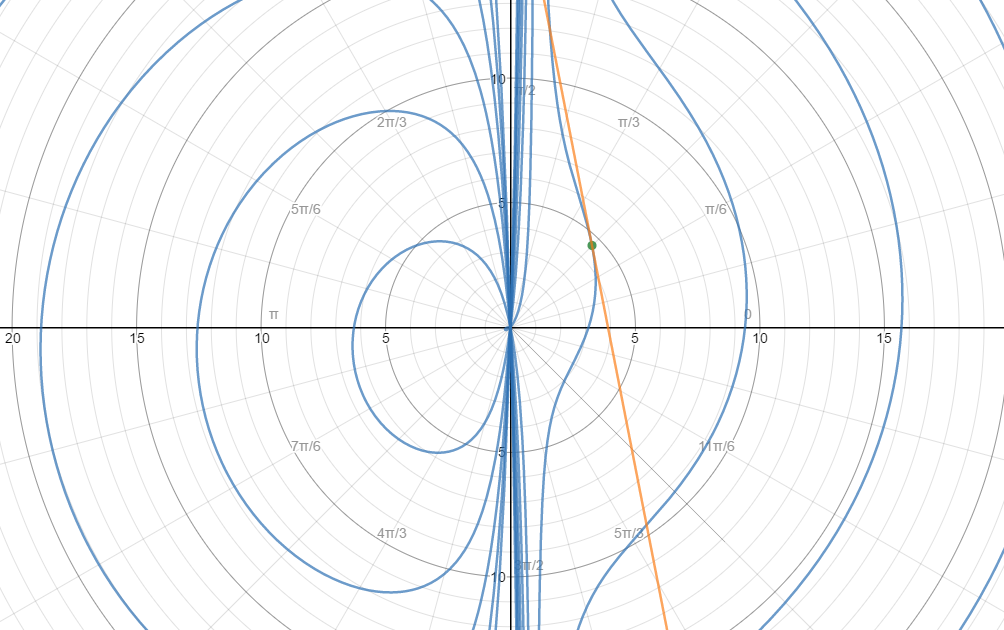
Here is a graph of the curve, the point of tangency, and the tangent line: