The solution:
The given
r=2theta-3 sin((13theta)/8-(5 pi)/3) at theta=(7pi)/6
dy/dx=(r cos theta+r' sin theta)/(-r sin theta+r' cos theta)
dy/dx=([2theta-3 sin((13theta)/8-(5 pi)/3)] cos theta+[2-3(13/8)cos ((13theta)/8-(5 pi)/3)]*sin theta)/(-[2theta-3 sin((13theta)/8-(5 pi)/3)] sin theta+[2-3(13/8)cos ((13theta)/8-(5 pi)/3)] cos theta)
Evaluating dy/dx at theta=(7pi)/6
dy/dx=([2((7pi)/6)-3 sin((13((7pi)/6))/8-(5 pi)/3)] cos ((7pi)/6)+[2-3(13/8)cos ((13((7pi)/6))/8-(5 pi)/3)]*sin ((7pi)/6))/(-[2((7pi)/6)-3 sin((13((7pi)/6))/8-(5 pi)/3)] sin ((7pi)/6)+[2-3(13/8)cos ((13((7pi)/6))/8-(5 pi)/3)] cos ((7pi)/6))
dy/dx=([(7pi)/3-3 sin((91pi)/48-(5 pi)/3)] cos ((7pi)/6)+[2-(39/8)cos ((91pi)/48-(5 pi)/3)]*sin ((7pi)/6))/(-[(7pi)/3-3 sin((91pi)/48-(5 pi)/3)] sin ((7pi)/6)+[2-(39/8)cos ((91pi)/48-(5 pi)/3)] cos ((7pi)/6))
color(blue)(dy/dx=([(7pi)/3-3 sin((11pi)/48)] cos ((7pi)/6)+[2-(39/8)cos ((11pi)/48)]*sin ((7pi)/6))/(-[(7pi)/3-3 sin((11pi)/48)] sin ((7pi)/6)+[2-(39/8)cos ((11pi)/48)] cos ((7pi)/6)))
color(blue)(dy/dx=-0.92335731861741)
x=r cos theta=(2theta-3 sin((13theta)/8-(5 pi)/3))*cos theta
x=[(7pi)/3-3 sin((91pi)/48-(5 pi)/3)] cos ((7pi)/6)
x=[(7pi)/3-3 sin((11pi)/48)] cos ((7pi)/6)
x=-4.6352670975528
y=r sin theta=(2theta-3 sin((13theta)/8-(5 pi)/3))*sin theta
y=[(7pi)/3-3 sin((91pi)/48-(5 pi)/3)] sin ((7pi)/6)
y=[(7pi)/3-3 sin((11pi)/48)] sin ((7pi)/6)
y=-2.6761727065385
Using Point-Slope Form:
Equation of the tangent line is
y-y_1=m(x-x_1)
y--2.6761727065385=-0.92335731861741(x--4.6352670975528)
Check the graph:
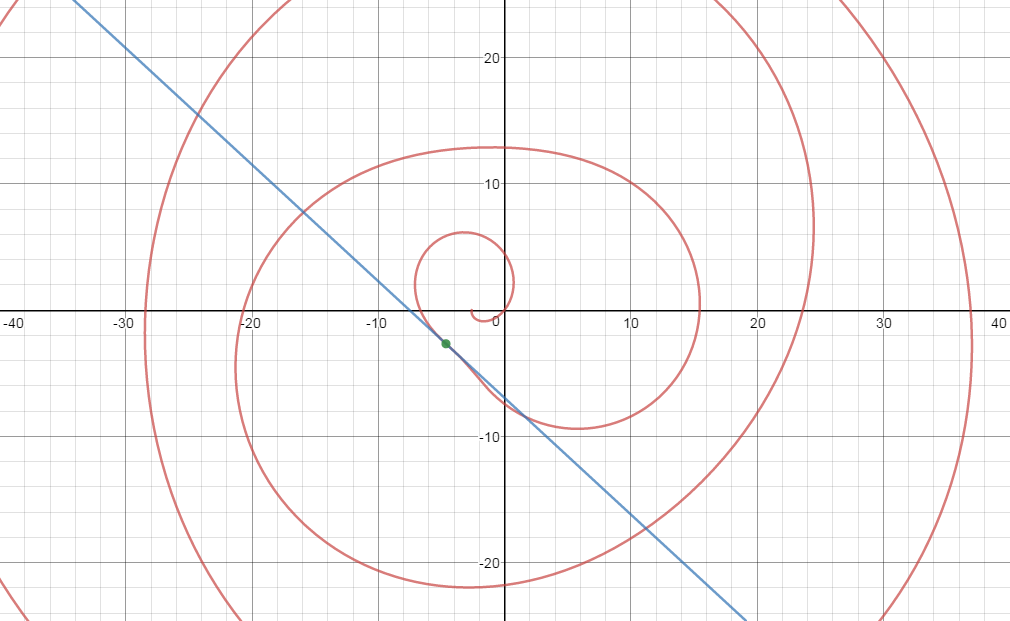 Desmos.com
Desmos.com
God bless....I hope the explanation is useful.
 Desmos.com
Desmos.com 