The reference Tangents with Polar Coordinates gives us this formula for #dy/dx#:
#dy/dx = ((dr)/(d theta)sin(theta) + rcos(theta))/((dr)/(d theta)cos(theta) - rsin(theta))" [1]"#
Substitute #theta - cos(-4theta+ (2pi)/3)# for every instance of r in equation [1]:
#dy/dx = ((dr)/(d theta)sin(theta) + (theta - cos(-4theta+ (2pi)/3))cos(theta))/((dr)/(d theta)cos(theta) - (theta - cos(-4theta+ (2pi)/3))sin(theta))" [2]"#
Substitute #1 - 4cos(pi/6 - 4theta)# for every instance of (dr)/(d theta) in equation [2]:
#dy/dx = ((1 - 4cos(pi/6 - 4theta))sin(theta) + (theta - cos(-4theta+ (2pi)/3))cos(theta))/((1 - 4cos(pi/6 - 4theta))cos(theta) - (theta - cos(-4theta+ (2pi)/3))sin(theta))" [3]"#
The slope, m, is equation [3] evaluated at #theta = (7pi)/4#:
#m = ((1 - 4cos(pi/6 - 7pi))sin((7pi)/4) + ((7pi)/4 - cos(-7pi+ (2pi)/3))cos((7pi)/4))/((1 - 4cos(pi/6 - 7pi))cos((7pi)/4) - ((7pi)/4 - cos(-7pi+ (2pi)/3))sin((7pi)/4))#
#m = 0.0564#
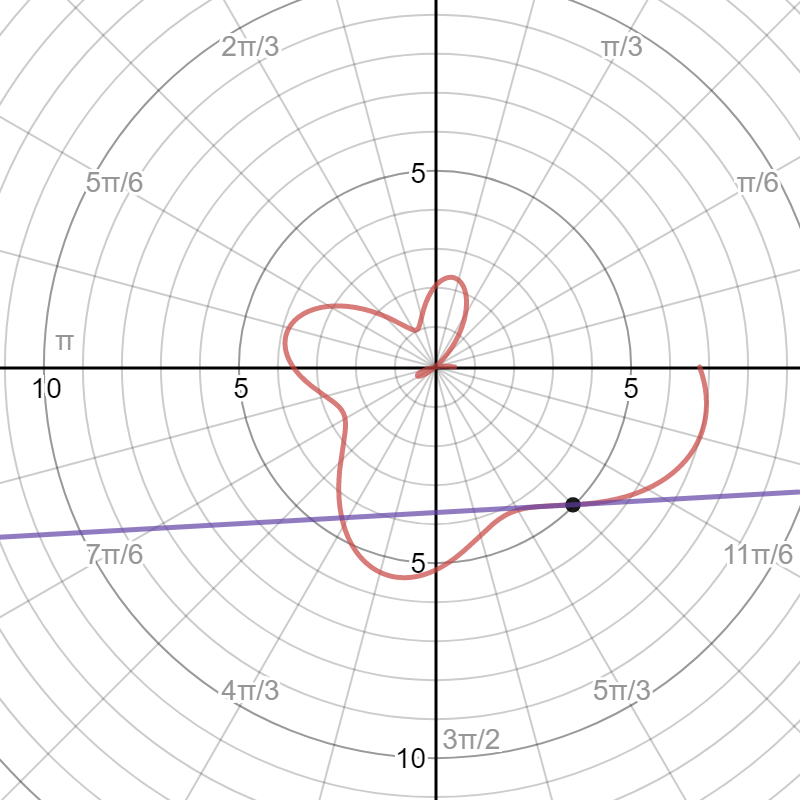
Here is a graph of r #0 <= theta < 2pi#, the specified point, and the tangent line with the above slope: