We need the equation
#dy/dx=((dr)/(d theta)sin(theta)+rcos(theta))/((dr)/(d theta)cos(theta)-rsin(theta))" [1]"#
from the reference Tangents with Polar Coordinates
I tried graphing #r=theta-cos(4theta-(3pi)/4); -2pi< theta <=0# but the Desmos.com/calculator would not graph it.
When I tried to graph #r=theta-cos(4theta-(3pi)/4); 0<= theta <2pi# the calculator plotted a graph but the point evaluated #theta_1 = -(2pi)/3# did not lie on the graph.
The only consistent graph occurred, when I converted #theta_1 to (4pi)/3# (the positive equivalent of #-(2pi)/3#).
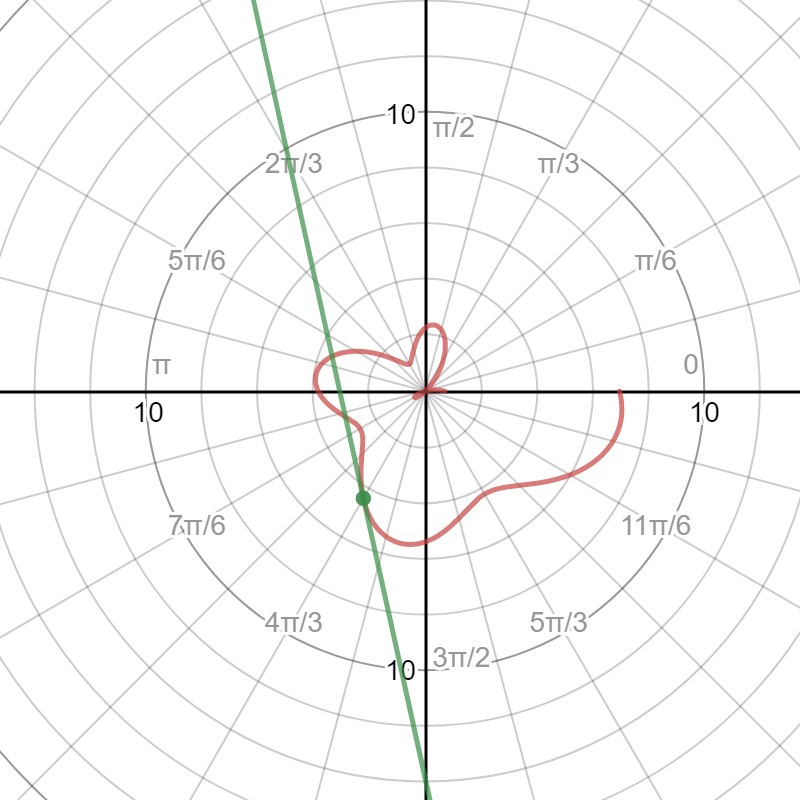
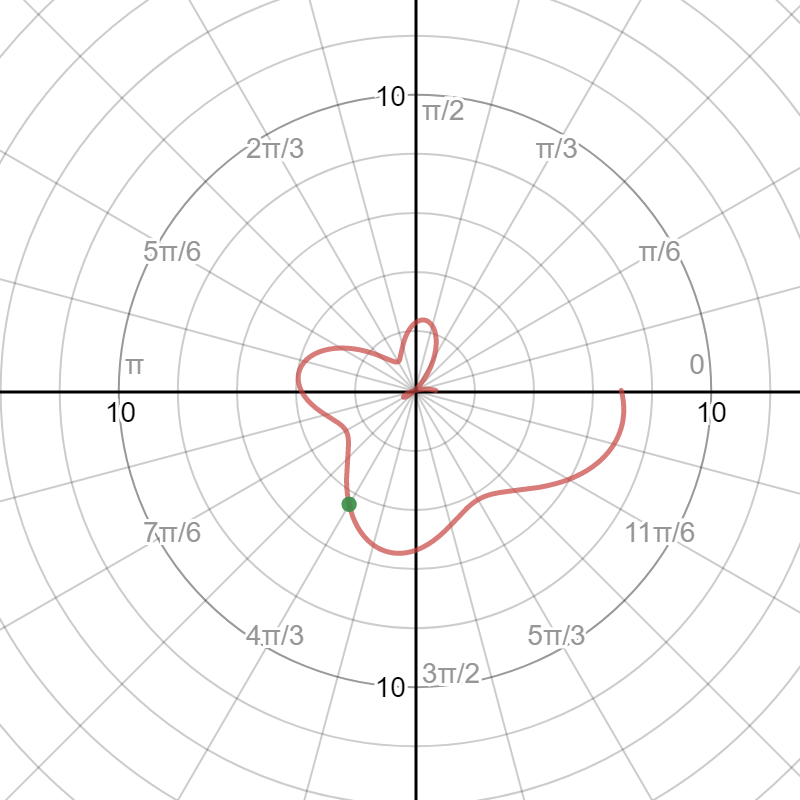
Here is the graph:
Compute #(dr)/(d theta)#:
#(dr)/(d theta) = 1 +4sin(4theta-(3pi)/4)#
Substitute #r and (dr)/(d theta)# into equation [1]:
#dy/dx=((1 +4sin(4theta-(3pi)/4))sin(theta)+(theta-cos(4theta-(3pi)/4))cos(theta))/(1 +4sin(4theta-(3pi)/4))cos(theta)-(theta-cos(4theta-(3pi)/4))sin(theta))" [2]"#
The slope, m, is equation [2] evaluated at #theta=(4pi)/3#:
#m=((1 +4sin(4((4pi)/3)-(3pi)/4))sin((4pi)/3)+((4pi)/3-cos(4((4pi)/3)-(3pi)/4))cos((4pi)/3))/(1 +4sin(4((4pi)/3)-(3pi)/4))cos((4pi)/3)-((4pi)/3-cos(4((4pi)/3)-(3pi)/4))sin((4pi)/3))" [3]"#
#m ~~ =-4.53#
I offer, as proof, a graph of the tangent line: