Question

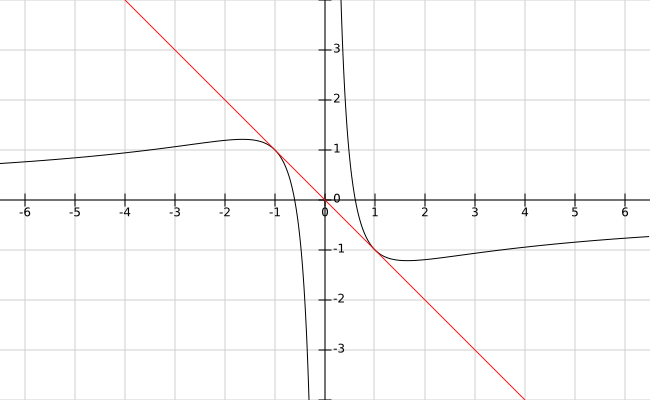
What is the slope of the tangent line of `x^2e^(xy)= C`, where C is an arbitrary constant, at `(-1,1)`?

Answer 1

The slope of the tangent is `m=-1`.

Explanation:

The slope of the tangent line to the curve is the value of the derivative `dy/dx` in the point `P(-1,1)`.

We can calculate the derivative using implicit differentiation:

`x^2e^(xy) = C`

Differentiate both sides with respect to `x`:

`2xe^(xy)+x^2e^(xy)(y+xdy/dx) = 0`

`xe^(xy)(2+xy+x^2dy/dx) = 0`

Now, `e^(xy) !=0` because the exponential is never null, and `x!=0` otherwise we would have `C=0`, and `y` indeterminate, which means for `C=0` the curve defined by the equation is the line `x=0` that does not pass through `P`. So:

`2+xy+x^2dy/dx = 0`

`dy/dx = -(2+xy)/x^2`

In the point `P(-1,1)` then the value of the derivative is:

`[dy/dx]_(-1,1) = -(2+(-1)*1)/(-1)^2 = -1`