What is the surface area of the solid created by revolving #f(x) =e^(2-4x^2) , x in [1,3]# around the x axis?
1 Answer
# S ~~ 0.114986857 ... #
Explanation:
Graphing the function we have:
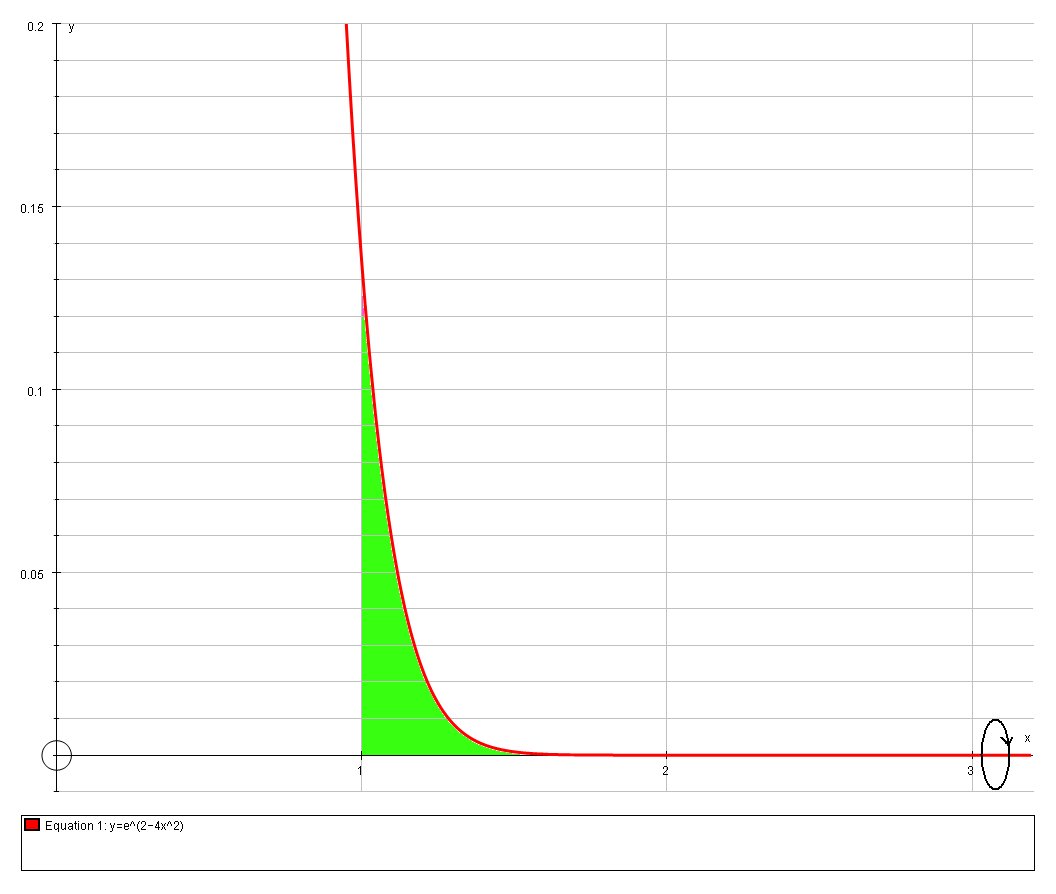
from the graph we can instantly establish that the bounded area is relatively small and so we predict the surface area of revolution will be also.
The Surface Area of Revolution about
# A = int_(alpha)^(beta) \ 2piy \ dS \ # where# \ dS = sqrt(1+(dy/dx)^2) \ dx#
This with the function
# f'(x) = e^(2-4x^2) * (-8x) = -8xe^(2-4x^2)#
So the required Surface Area is given by:
# S = int_(1)^(3) \ 2pi e^(2-4x^2) \ sqrt(1+(-8xe^(2-4x^2))^2) \ dx#
# \ \ = int_(1)^(3) \ 2pi e^(2-4x^2) \ sqrt(1 + 64x^2e^(4-8x^2)) \ dx#
As is typical with these types of questions, we cannot evaluate this integral usiung standard mathematical techniques or functions. We can however use Numerical; Techniques and we find that
# S ~~ 0.114986857 ... #
Which is relatively small consistent with the initial predictions

