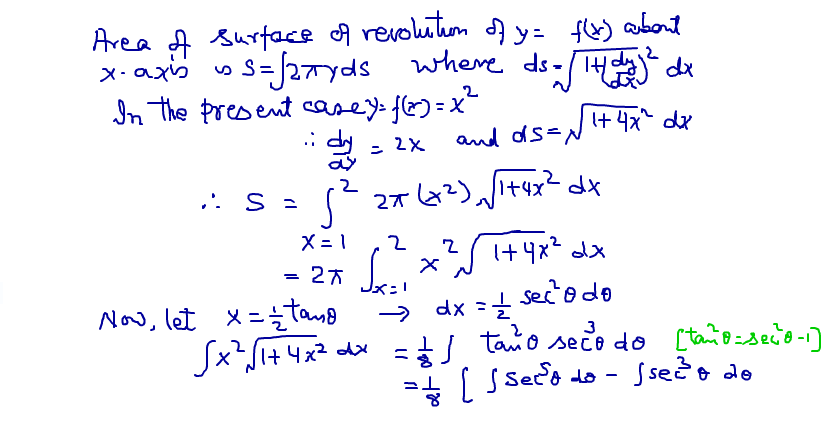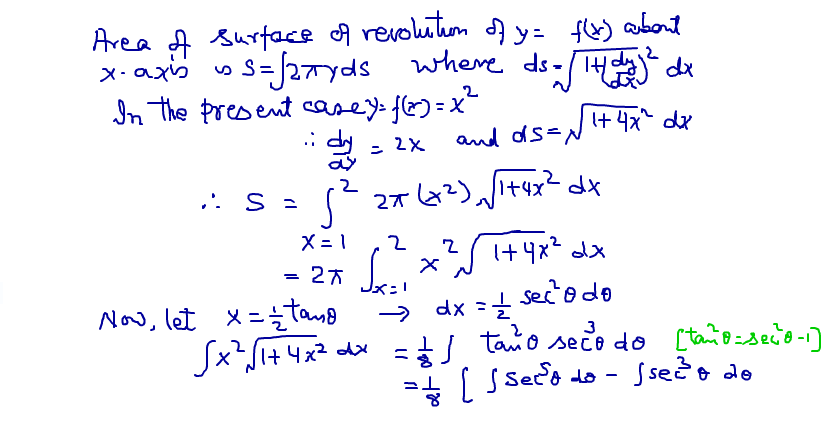
Now, integrating by parts #int sec^3 theta=int sec theta sec^2 theta d theta#
=#sectheta int sec^2 theta d theta - int sec theta tan theta int sec^2 theta d theta #
=#sec theta tan theta -int sec theta tan^2 theta d theta#
=#sec theta tan theta - int sec^3 theta d theta +int sec theta d theta#
Now transposing #int sec^3 theta d theta #to the left side and integrating #sec theta d theta#,
#2int sec^3 theta d theta= sec theta tan theta +ln|sec theta +tan theta|#
Thus #int sec^3 theta d theta=1/2 sec theta tan theta +1/2 ln |sec theta + tan theta| #
Like wise, using technique of integration by parts #int sec^5 theta d theta= int sec^3 theta sec^2 theta d theta = sec^3 theta int sec^2 theta d theta - int (3sec^2 theta sec theta tan theta) int (sec^2 theta) d theta#
=#sec^3 theta tan theta-3 int sec^3 theta tan^2 theta d theta#
=#sec^3 theta tan theta -3int (sec^5 theta -sec^3 theta d theta)#
Now transpose #int sec^5 theta d theta# to the right side to get
#int sec ^5 theta d theta = 1/4 sec^3 theta tan theta + 3/4 int sec^3 theta d theta#
Now using the integral of #sec^3 theta# derived earlier,
#int x^2 sqrt (4x^2 +1) dx= 1/8[ int sec^5 theta d theta - int sec^3 theta d theta]=1/8[ 1/4 sec^3 theta tan theta -1/4 int sec^3 theta d theta]#
=#1/32[sec^3 theta tan theta -1/2 sec theta tan theta -1/2 ln|sec theta +tan theta|]#
Now substituting theta by x it would be #tan theta =2x# and #sec theta= sqrt(4x^2 +1)#
#int x^2 sqrt (4x^2 +1) dx = 1/16 x (4x^2+1)^(3/2)-1/32 x sqrt (4x^2+1) -1/64 ln |sqrt (4x^2 +1) +2x| #
The required surface area would thus be
#2 pi[ 1/16 x (4x^2+1)^(3/2)-1/32 x sqrt (4x^2+1) -1/64 ln |sqrt (4x^2 +1) +2x|]_1^2 #
=#2pi[1/8 17^(3/2) -1/16 sqrt 17 -1/64 ln|sqrt 17 +4| -1/16 5^(3/2) +1/32 sqrt 5 +1/64 ln |sqrt 5 +2|]#
*****