What is the surface area produced by rotating #f(x)=1/(x^2+1), x in [0,3]# around the x-axis?
1 Answer
Aug 3, 2017
Well, the surface area of a function
#S = int 2pi f(x)ds#
#= int overbrace(2pi f(x))^"Circumference"overbrace(sqrt(1 + ((df)/(dx))^2))^("Arc Length")dx#
This surface would look like:
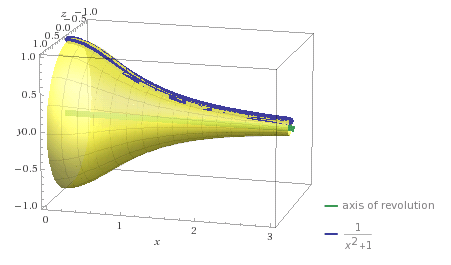
First we get the derivative.
#(df)/(dx) = -(2x)/(x^2 + 1)^2#
And square it to get:
#((df)/(dx))^2 = (2x)^2/(x^2 + 1)^4#
So, the surface area integral is:
#S = 2pi int_(0)^(3) 1/(x^2 + 1)sqrt(1 + ((2x)^2)/(x^2 + 1)^4)dx#
#= 2pi int_(0)^(3) sqrt(1/(x^2 + 1)^2 + ((2x)^2)/(x^2 + 1)^6)dx#
There is no elementary solution to this, so we can only get the numerical integration result,

