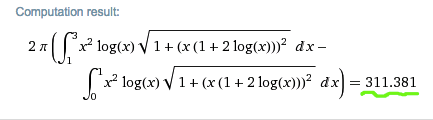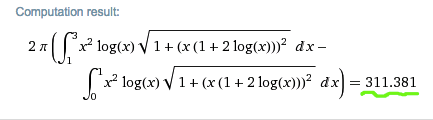If we consider a small strip width #dx#, it will have radius #y(x)# as it is revolved about the x axis, and thus circuference #2 pi y#.
The arc length #ds# of the tip of strip #dx# is:
#ds = sqrt ( 1 + (y')^2) dx#
With # y' = x(1 + 2 ln x)##
and so the surface area of the element is
#dS = 2 pi y ds #
#= 2 pi x^2 ln x sqrt ( 1 + ( x(1 + 2 ln x))^2) dx#
For #x in [1,3]#, the surface area #S# is therefore:
#S = 2 pi int_1^3 \ x^2 ln x sqrt ( 1 + ( x(1 + 2 ln x))^2) dx#
However because #y < 0# for #x in [1,3]#, which would generate a negative radius, we need to be sure to place a negative number on the integration.
The surface area in total is therefore
#S = 2 pi ( int_1^3 \ x^2 ln x sqrt ( 1 + ( x(1 + 2 ln x))^2) dx - int_0^1 \ x^2 ln x sqrt ( 1 + ( x(1 + 2 ln x))^2) dx )#