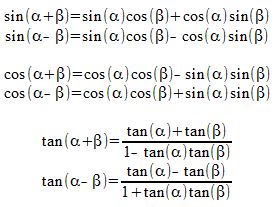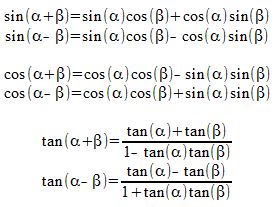Recall that #15˚# can be written as #60˚ - 45˚#.
So, #tan15˚ = tan(60˚ - 45˚)#. We have to expand this using the difference formula for tangent. The sum/difference formulas are shown in the following table.
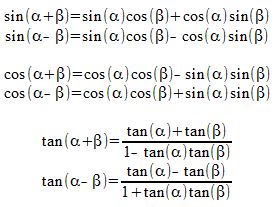
#tan(60˚ - 45˚) = (tan60˚- tan45˚)/(1 + tan60˚tan45˚)#
#tan(60˚ - 45˚) = (sqrt(3) - 1)/(1 + sqrt(3) xx 1)#
#tan(15˚) = (sqrt(3) - 1)/(1 + sqrt(3)#
It is preferable that the denominator is rationalized.
#tan15˚ = (sqrt(3) - 1)/(1 + sqrt(3)) xx (1 - sqrt(3))/(1 - sqrt(3))#
#tan15˚ = (sqrt(3) + sqrt(3) - 1 - sqrt(9))/(1 - sqrt(9))#
#tan15˚ = (2sqrt(3) - 4)/(-2)#
#tan15˚ = (2(sqrt(3) - 2))/-2#
#tan15˚ = -(sqrt(3) - 2)#
#tan15˚ = 2 - sqrt(3)#
Hopefully this helps!