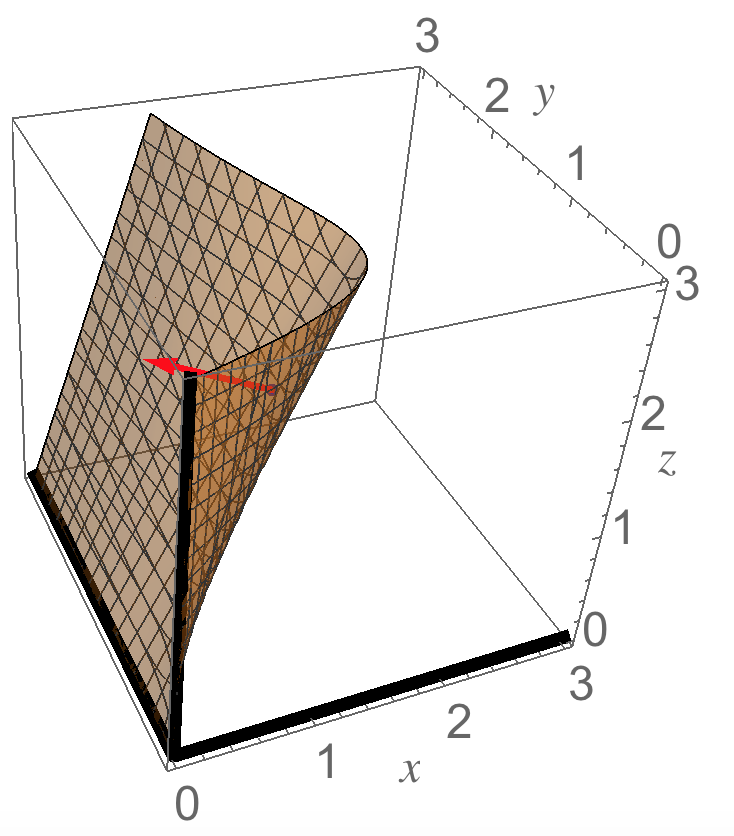
Rewrite the equation #z=xy+x/y# as #xy+x/y-z=0# and let #F(x,y,z)=xy+x/y-z# so that the equation is #F(x,y,z)=0#.
The gradient vector of #F# is normal to the surface at any given point on the surface. That gradient vector is
#nabla F=< (partial F)/(partial x), (partial F)/(partial y), (partial F)/(partial z)> = < y+1/y,x-x/y^2,-1>#.
At the point #(x,y,z)=(1,1,2)# (which you should check is on the original surface), this gradient vector is #nabla F=<2,0,-1>#.
Since #||nabla F||=sqrt{2^{2}+0^{2}+(-1)^{2}}=sqrt{5}#, it follows that #vec(n)=-(nabla F)/||nabla F||=<-2/sqrt(5),0,1/sqrt(5)> = -2/sqrt(5) hat(i)+1/sqrt(5) hat(k)# is a unit vector normal to this surface with a positive #z#-component.
Here's a picture of this situation: