What is the vertex of #f(x)=7-x^2#?
4 Answers
The vertex is
Sometimes we have problems with the easier questions because it's not exactly in the form we're used to. Normally for a quadratic, you would complete the square to find the vertex. But this quadratic is already in vertex or standard form:
#f(x)=-(x-0)^2+7#
We can also find the vertex by using the expressions:
#(-b/(2a), f(-b/(2a)))#
Standard form:
#ax^2+bx+c=0#
In this example,
#x=−0/(2(−1))=0/2=0#
#y=f(0)=7−0^2=7#
Same result of
Yes, the vertex is at (0,7), but I would like to address this problem graphically.
The graph of a function
When you consider a graph of a function
Next we transform our function into
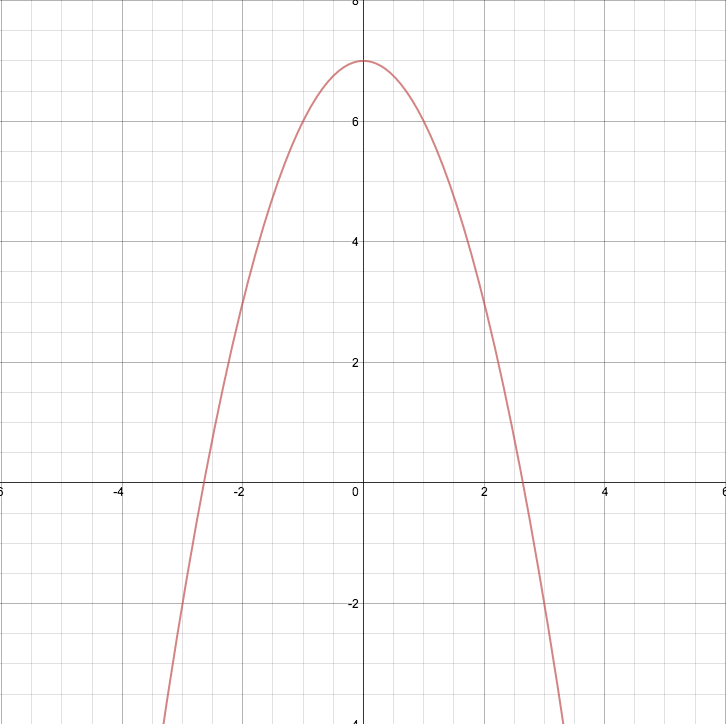
We could also use Calculus to solve this question.
We have to recognize that this is a quadratic equation which is just a parabola.
We know that a parabola will have either a maximum or minimum at the vertex.
The derivative of a function is the slope of the tangent line at a specific point on the function.
The derivative or tangent line at the vertex will have a slope of 0.
Set the derivative equal to zero to find the
The
Now substitute in
The vertex is at point




