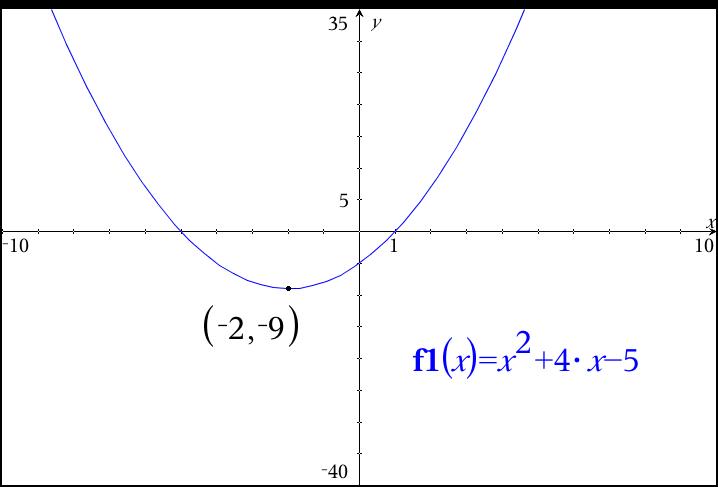
What is the vertex of f(x)=x^2+4x-5f(x)=x2+4x−5?

1 Answer
MrsRudolph221
Sep 4, 2014

There are several ways to find the vertex of a parabola:
1. Complete the square
2. Use frac{-b}{2a}−b2a
3. Find the average of the two x-intercepts, and substitute that x-value in to find the y-value. (f(x))
4. Use a graphing calculator and the "analyze" feature

  1. Here is how I would complete the square:
    Replace f(x) with "y" and make sure that the lead coefficient = 1
    y = x^2+4x - 5y=x2+4x−5
    y + 5 = x^2 + 4xy+5=x2+4x
    y + 5 + ???_ = x^2x2 + 4x + _???__

(take half of the coefficient of the x-term, then square it)
so y + 5 + 4 = x^2x2 + 4x + 4
y + 9 = (x +2)^2(x+2)2 (the right side is a perfect square trinomial!)
Then set y + 9 = 0 and x + 2 = 0 to get y = -9 and x = -2 which are the coordinates of the vertex (-2, -9).

Method 2 involves calculating frac{-b}{2a}−b2a from your standard form equation as given. That is, a = 1, b = 4 and c = -5.
x = frac{-4}{(2*1)}−4(2⋅1) = frac{-4}{2}−42 = -2.

Now that you have the x-value for the vertex, substitute it into the function and find f(-2) = (-2)^2+4(-2)-5(−2)2+4(−2)−5 = 4 + (-8) - 5 = -9.

Confirmed, (-2,-9) is the vertex.

Method 3. This quadratic is factorable: x^2+4x-5=(x+5)(x-1)x2+4x−5=(x+5)(x−1)
So the zeros are x = -5 and 1. Average the zeros: frac{-5+1}{2}−5+12 = frac{-4}{2}−42 = -2. Repeat finding f(-2) to get -9.

Method 4 involves using technology and not showing any work to your instructor. Is this really how you want to do it? Here is what my calculator would show:my screenshot

Related questions
See all questions in Graphing Quadratic Functions
Impact of this question
27381 views around the world
You can reuse this answer
Creative Commons License