Question

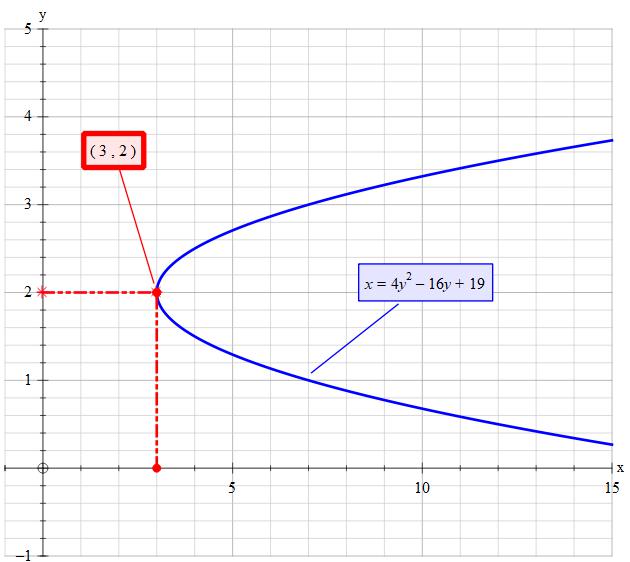
What is the vertex of `x – 4y^2 + 16y – 19 = 0`?

Answer 1

Vertex `->(x,y)=(3,2)`

Explanation:

This is a quadratic in `y` instead of `x`. Thus the graph is like one done in `x` but rotated `90^0`. So you would have an axis of symmetry that is parallel to the y-axis.

As the coefficient of `y^2` is positive the graph is of form `sub`

Write as `x=4y^2-16y+19" "............. Equation(1)`

Now write as `x=4(y^2-16/4x)+19" ".................Equation(1_a)`

Normally I would use the cheat of
`x_("vertex")=(-1/2)xxb/a`

However in this case we have
`y_("vertex")=(-1/2)xx(-16/4) = +2`

Note that this is part of the process of completing the square.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
So by substitution for `y`

`x_("vertex")=4(+2)^2-16(+2)+19 = 3`

Vertex `->(x,y)=(3,2)`