Question

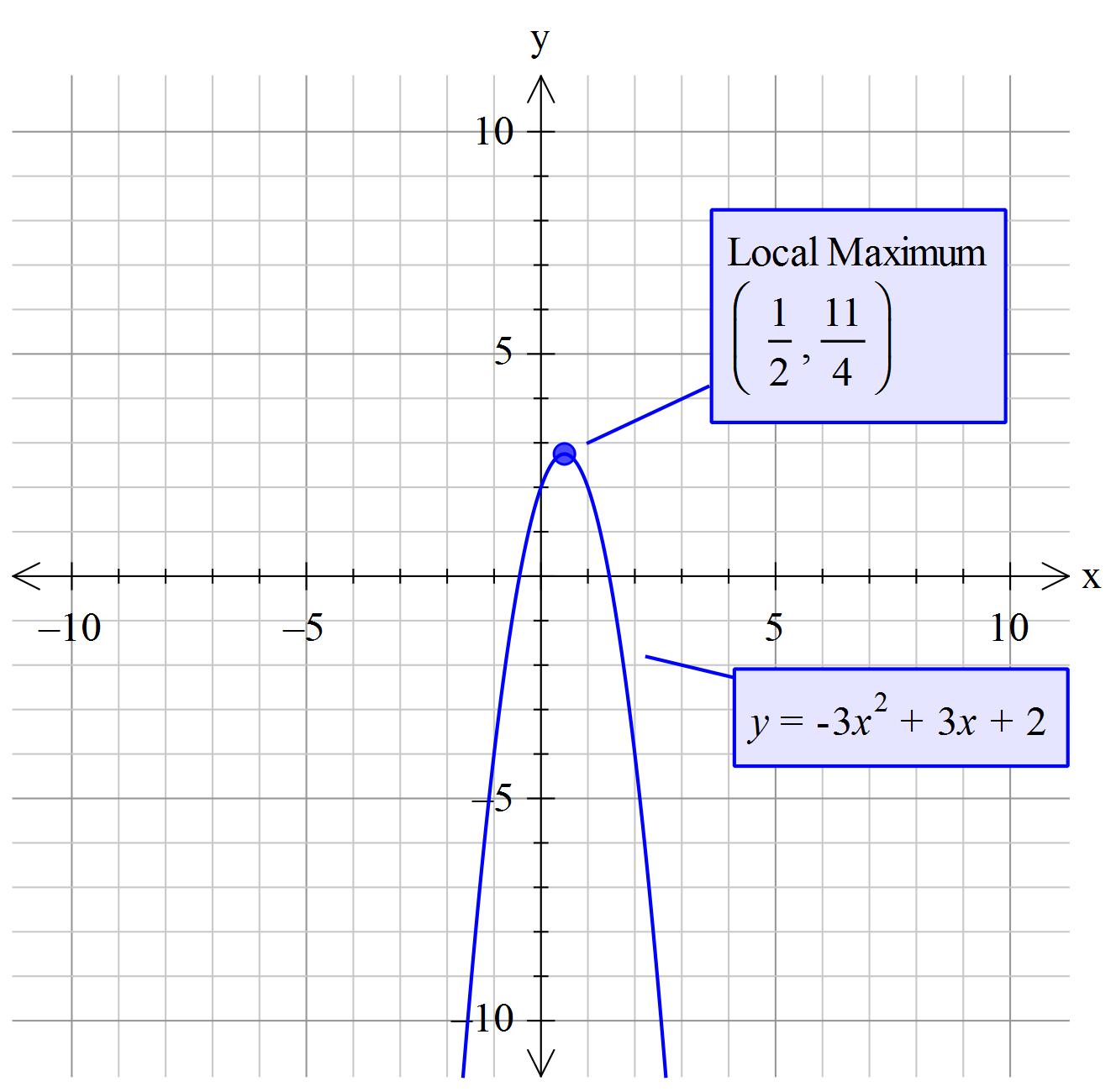
What is the vertex of `y= -(2x-1)^2+x^2-x+3`?

Answer 1

`"vertex "->(x,y)->(1/2,11/4)`

Explanation:

Multiply out the brackets giving:

`y=-(4x^2-4x+1)+x^2-x+3`

Multiply everything inside the bracket by `(-1)` giving

`y=-4x^2+4x-1+x^2-x+3`

`y=-3x^2+3x+2`

Write as: `y=-3(x^2+3/(-3)x)+2`

`=>y=-3(x^2-x)+2`

Consider the coefficient `-1` from `-x` inside the brackets

`color(blue)(x_("vertex")=(-1/2)xx(-1)=+1/2)`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Substitute for #x_("vertex") in the equation

`color(brown)(y=-3x^2+3x+2" "->" " y=-3(color(blue)(1/2))^2+3(color(blue)(1/2) )+2`

`color(blue)(y_("vertex")= 2 3/4 = 11/4)`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`color(blue)("vertex "->(x,y)->(1/2,11/4)`