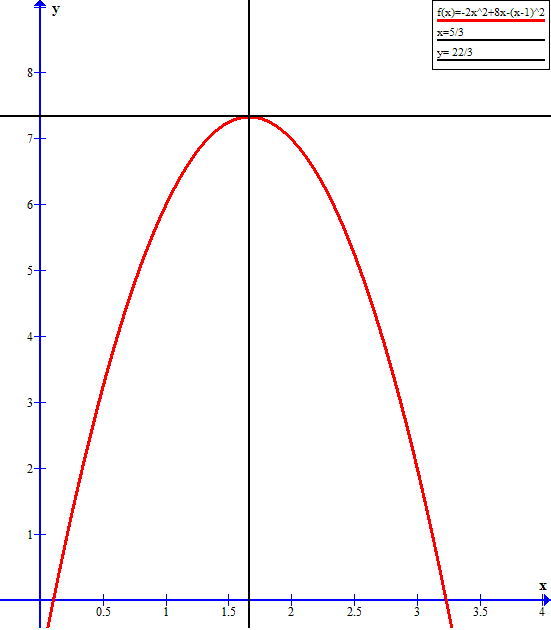
Convert the given equation #y=-2x^2+8x-(x-1)^2#
into vertex form:
#color(white)("XXX")y=color(green)m(x-color(red)a)^2+color(blue)b# with vertex at #(color(red)a,color(blue)b)#
#y=-2x^2+8x-(x-1)^2#
#color(white)("XXX")=-2x^2+8x-x^2+2x-1#
#color(white)("XXX")=-3x^2+10x-1#
#color(white)("XXX")=color(green)(-3)(x^2-10/3x)-1#
#color(white)("XXX")=color(green)(-3)(x^2-10/3x+((cancel(10)^5)/(cancel(6)_3))^2)-1-(color(green)(-3)) * (5/3)^2#
#color(white)("XXX")=color(green)(-3)(x-color(red)(5/3))^2-1+25/3#
#color(white)("XXX")=color(green)(-3)(x-color(red)(5/3))^2+color(blue)(22/3)#
which is the vertex form with the vertex at
#color(white)("XXX")(color(red)(5/3),color(blue)(22/3))=(color(red)(1 2/3),color(blue)(7 1/3))#