Question

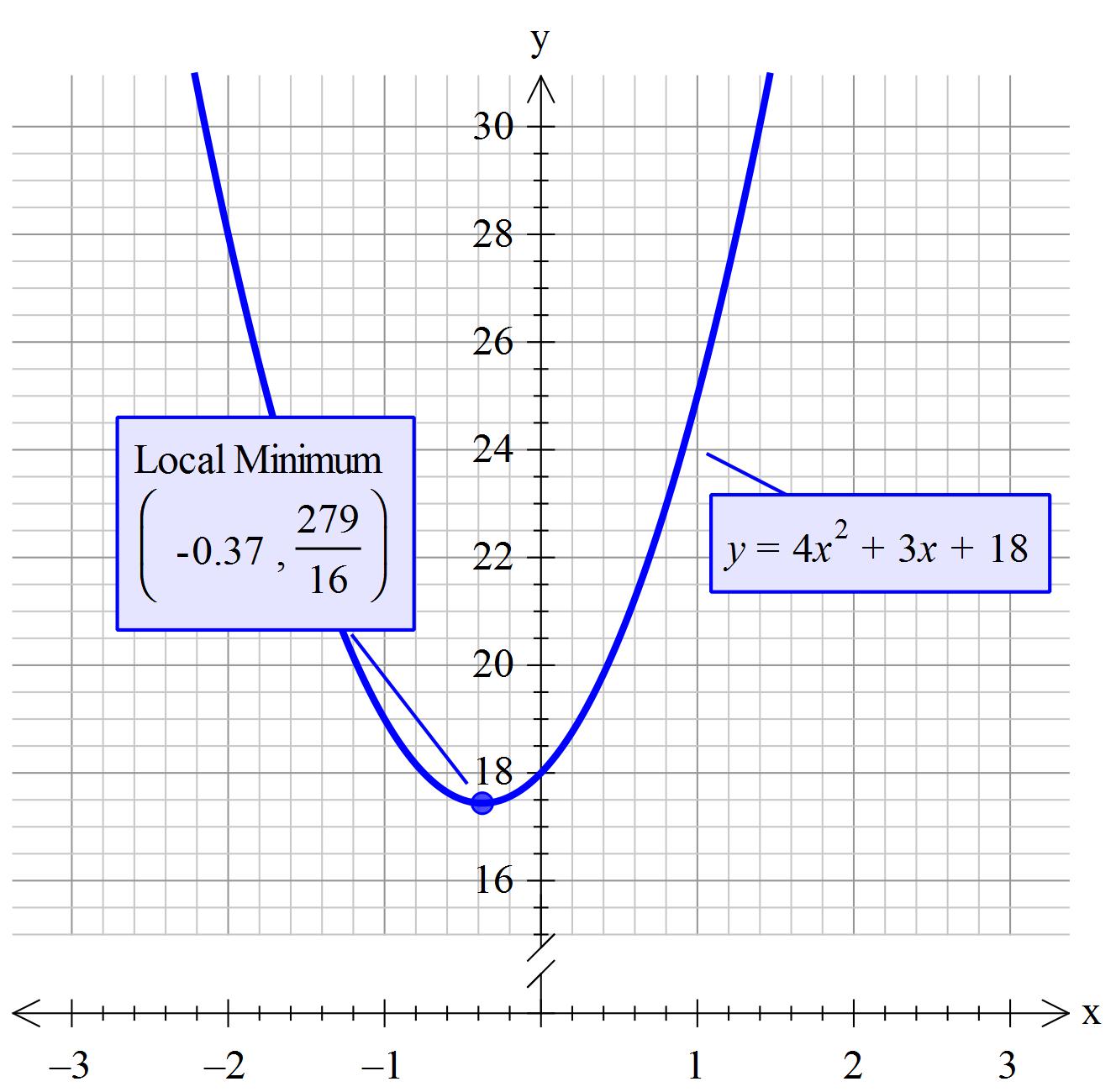
What is the vertex of `y=4x^2+3x+18`?

Answer 1

`color(green)("Vertex"->(x,y)->(-3/8,279/16)`

Notice the way I stick with fractions. Much more pricise than decimals.

Explanation:

There are various ways of doing this. I am going to show you one of them.

Write the equation as:

`y=4(x^2+3/4x)+18`

`color(blue)("Determine "x_("vertex"))`
Multiply the `3/4` by `(-1/2)`

`color(blue)(x_("vertex")=(-1/2)xx3/4= -3/8)`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Not that `-3/8 =0.375`
My graphing package has not rounded this properly to 2 decimal places
'|~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`color(blue)("Determine "y_("vertex"))`

Substitute of `x`

`y_("vertex")=4(-3/8)^2+3(-3/8)+18`

`y_("vertex")=4(+9/64)-9/8+18`

`color(blue)(y_("vertex")=9/16-9/8+18 = 279/16)`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(green)("Vertex"->(x,y)->(-3/8,279/16)`