Question

What type of conic section has the equation `9y^2 - x^2 - 4x+54y +68= 0`?

Answer 1

`9y^2−x^2−4x+54y+68=0` will have a hyperbola for its graph.

How do I know? Just a quick check of the coefficients on the `x^2` and the `y^2` terms will tell...
1) if the coefficients are both the same number and the same sign, the figure will be a circle.
2) if the coefficients are different numbers but the same sign, the figure will be an ellipse.
3) if the coefficients are of opposites signs, the graph will be a hyperbola.

Let's "solve" it: `-1(x^2 +4x) + 9(y^2+6y) = -68`
Notice that I factored out the leading coefficients already, and gathered together the terms that both have the same variable.

`-1(x^2+4x+4)+9(y^2+6y+9) = -68 + -1(4) + 9(9)`
In this step, I completed the square by adding 4 and 9 inside of the parentheses, but then added to the other side, those numbers multiplied by the factored out numbers -1 and 9.

`-1(x+2)^2+9(y+3)^2=9` Rewrite in factored forms on the left.

`-1(x+2)^2/9+(y+3)^2/1=1` which just looks awkward...so I will change the order and make it look like subtraction:

`(y+3)^2-(x+2)/9 = 1`
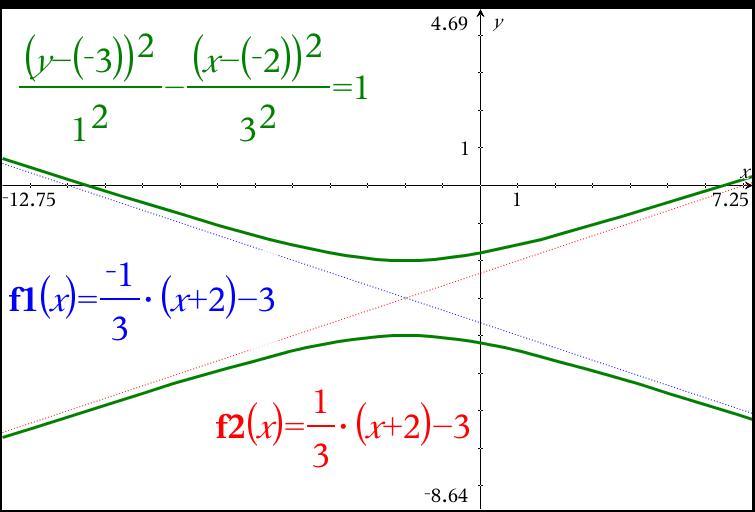
That is what I wanted to see; I can tell what the center of the hyperbola is (-2,-3), how far to move from center to get to vertices (up and down 1 unit since the y-term is divided by 1) and the slope of the asymptotes (`+-1/3`) . The "flatness" of this slope, in addition to the upward and downward opening of the curves, will make this graph fairly wide open.