General Form of the Equation
Key Questions
-
I can not remember how to deal with
#xy# so I will be demonstrating completing the square without one.Consider the equation below
#9x^2 -16y^2 -36x - 96y - 252 = 0#
The first thing that we should do is group our
#x# s and#y# s#9x^2 -16y^2 -36x - 96y - 252 = 0#
#=> (9x^2 -36x) + (-16y^2 - 96y) - 252 = 0# Now, let's make our work easier by factoring out
#x^2# 's and#y^2# 's coefficient#(9x^2 -36x) + (-16y^2 - 96y) - 252 = 0# #=> 9(x^2 - 4x) + -16(y^2 + 6y) - 252 = 0#
Before proceeding, let's recall what happens when a binomial is squared
#(ax + b)^2 = a^2x^2 + 2ab + b^2# when a = 1, we have
#(x + b)^2 = x^2 + 2b + b^2#
Now, in our equation,
#9(x^2 - 4x) + -16(y^2 + 6y) - 252 = 0# We want
#x^2 - 4x# and#y^2 + 6y# to be perfect squares.
In order to do that, we need to add a 3rd element.We know that in
#x^2 - 4x# ,#2b = -4 #
#b = -2# For
#x^2 - 4x# to be a perfect square, we need to add#b^2 = 4# Meanwhile, for
#y^2 + 6y# ,#2b = 6#
#b = 3# For
#y^2 + 6y# to be a perfect square, we need to add#b^2 = 9#
#9(x^2 - 4x) + -16(y^2 + 6y) - 252 = 0# #=> 9(x^2 - 4x + 4) + -16(y^2 + 6y + 9) - 252 = 0# We added something in the left-hand side of the equation.
Since we our dealing with an equality, we need to maintain the
equality.
We can do this by adding the same value in the right-hand side of the equation or by subtracting the same value in the left-hand side.For this demonstration, I will subtract the same value in the left-hand side
#=> 9(x^2 - 4x + 4) + -16(y^2 + 6y + 9) - 252 = 0# #=> 9(x^2 - 4x + 4) + -16(y^2 + 6y + 9) - 252 - 9(4) - -16(9) = 0# Now that we have our perfect square trinomials and our equality remains to be one, we can proceed to simplifying the equation
#9(x^2 - 4x + 4) + -16(y^2 + 6y + 9) - 252 - 9(4) - -16(9) = 0# #=> 9(x - 2)^2 + -16(y + 3)^2 - 252 - 9(4) - -16(9) = 0#
#=> 9(x - 2)^2 + -16(y + 3)^2 - 252 - 36 - -144 = 0#
#=> 9(x - 2)^2 + -16(y + 3)^2 - 144 = 0#
#=> 9(x - 2)^2 + -16(y + 3)^2 = 144# #=> (9(x - 2)^2 + -16(y + 3)^2 = 144)/144# #=> (9(x - 2)^2)/144 + (-16(y + 3)^2)/144 = 144/144# #=> ((x - 2)^2)/16 + (-(y + 3)^2)/9 = 1# #=> (x - 2)^2/16 - (y + 3)^2/9 = 1# Now we have transformed our general equation to standard form.
Take note that we can do the same trick to transform other conic sections into their standard form. -
Let us find the slant asymptotes of a hyperbola of the form
#x^2/a^2-y^2/b^2=1# .By subtracting
#x^2/a^2# ,#=>-y^2/b^2=-x^2/a^2+1# by multiplying by
#-b^2# ,#=> y^2=b^2/a^2 x^2-b^2# by taking the square-root,
#=> y=pm sqrt{b^2/a^2 x^2-b^2}# For large
#x# ,#-b^2# in the square-root is negligible,#y=pm sqrt{b^2/a^2 x^2-b^2}approx pm sqrt{b^2/a^2 x^2}=pm b/a x# Hence, the slant asymptotes are
#y=pm b/a x# .
I hope that this was helpful.
-
Well a hyperbola will look something like this:
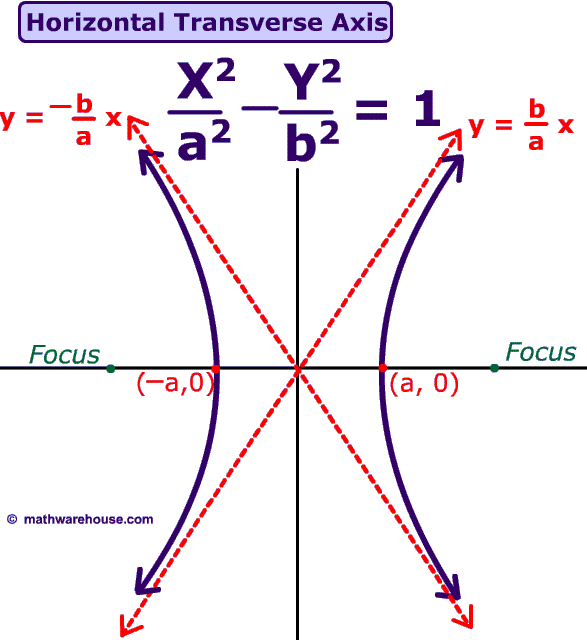
So in general terms we can say that an hyperbolic equation will be in the terms
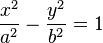
or
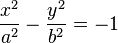
So you can see also from this that it may be in a form like this:
#(x/a + y/b)(x/a - y/b) = 1# or
#(x/a + y/b)(x/a - y/b) = -1# -
The general form of a hyperbola is
#Ax^2 + Bx + Cy^2 + Dy + E = 0# where either A or C is negative (but never both)