Which of the following set of quantum numbers is not allowed?
A) #n=1, l=0, m_l=0, m_s=-1/2#
B) #n=3,l=2, m_l=-1, m_s=1/2#
C) #n=5, l=2, m_l=-3, m_s=-1/2#
D) #n=4, l=3, m_l=-2, m_s=1/2#
A)
B)
C)
D)
1 Answer
The answer is C).
Explanation:
All you have to do here is to use the definitions of the four quantum numbers that we use to describe the location and spin of an electron inside an atom.
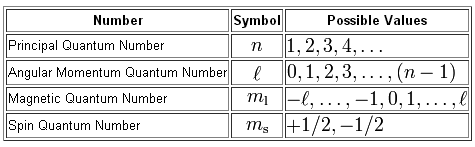
Notice that the magnetic quantum number,
#m_l = {-l, -(l+1), ..., -1, 0 ,1, ..., (l+1), l}#
This tells you that the absolute value of the magnetic quantum number cannot exceed the value of the angular momentum quantum number
#|m_l| <= l#
For option C), you have
#|-3| color(red)(cancel(color(black)( <=))) 2#
In other words, the
#m_l = { -2, -1, 0, 1, 2} -># for the d subshell
Therefore, you can say that
#n=5, l = 2, m_l = -3, m_s = -1/2#
is not a valid set of quantum numbers.
The other three sets of quantum numbers are indeed valid.
#n=1, l=0, m_l = 0, m_s = -1/2# Describes an electron located on the first energy level, in the s subshell, in the
#1s# orbital, that has spin-down
#n=3, l=2, m_l = -1, m_s = 1/2# Describes an electron located on the third energy level, in the d subshell, in one of the five
#3d# orbitals, that has spin-up
#n=4, l=3, m_l = -2, m_s = 1/2# Describes an electron located on the fourth energy level, in the f subshell, in one of the seven
#4f# orbitals, that has spin-up

