Which type of transformation does not preserve orientation?
1 Answer
Reflection does not preserve orientation.
Dilation (scaling), rotation and translation (shift) do preserve it.
Explanation:
Perfect example of "oriented" figure on a plane is the right triangle
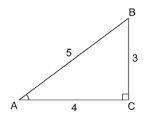
To introduce orientation, let's position ourselves above the plane and, looking down on this triangle, notice that the way from vertex
Rotation, translation (shift) or dilation (scaling) won't change the fact that the direction
Use now a reflection of this triangle relative to some axis. For instance, reflect it relative to a line
The way

