A higher oxidation state means the transition metal is more electropositive, so it draws more electron density towards itself (relative to a metal with a lower oxidation state).
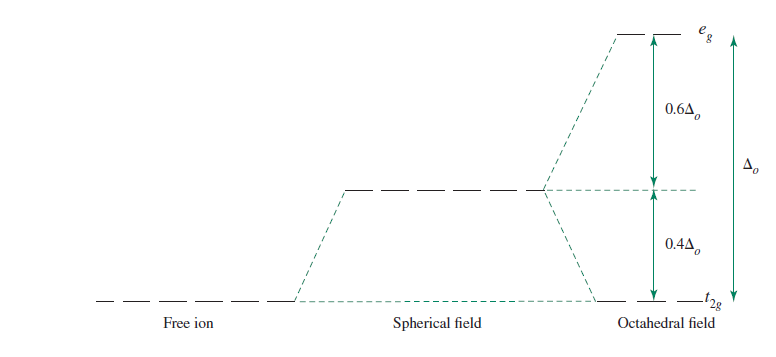
That means there are more repulsions within the #d# atomic orbitals, not less. From the point of view of crystal field theory, it means that the crystal field splitting energy increases.
This is only because the ligands are assumed to only donate electron density. That is, the #t_(2g)# orbitals can apparently never get any lower in energy than the free-ion #d# orbital energies (which isn't true in real life).
IMPORTANT NOTE:
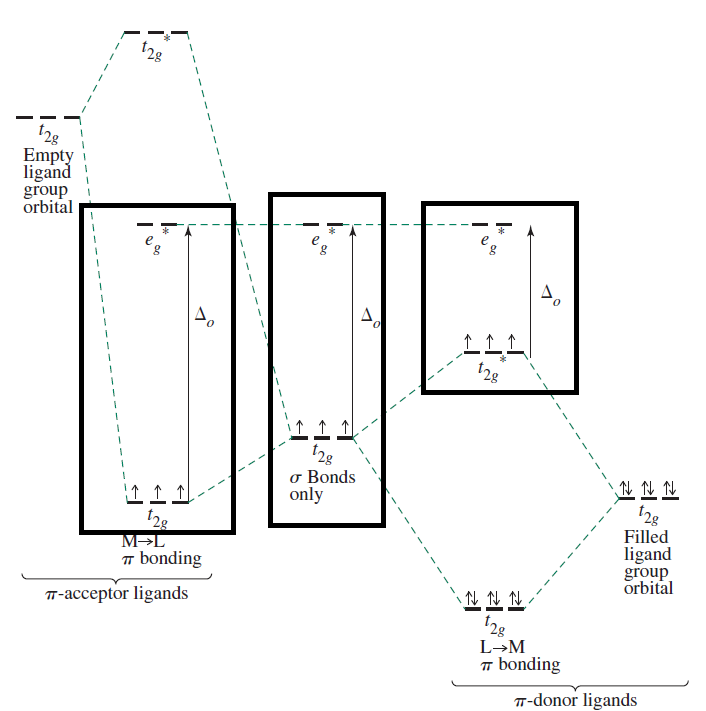
In terms of #sigma# donors, they then donate more electron density into the metal #d_(x^2-y^2)# and #d_(z^2)# orbitals (#sigma#-bonding atomic orbitals), which increases the energy of the #e_g^"*"# antibonding orbitals, which increases the splitting energy.
This is accounted for in crystal field theory.
In terms of #pi# donors, they then donate electron density into the metal #d_(xy)#, #d_(xz)#, and #d_(yz)# orbitals, which increases their energies relative to no interaction.
With a higher metal oxidation state, more #pi# donation occurs into the metal from the ligand, so this technically means the #t_(2g)# orbital energies increase, and thus the splitting energy decreases.
Crystal field theory does not account for this. So, we ignore this in crystal field theory.
In terms of #pi# acceptors, they normally accept electron density from the metal #d_(xy)#, #d_(xz)#, and #d_(yz)# orbitals. With a higher metal oxidation state, there is less metal-to-ligand backbonding, which technically means the stabilizing effect of backbonding is less, and thus the #t_(2g)# orbitals are less lowered in energy and the splitting energy decreases.
This is not accounted for in crystal field theory either, and we ignore this until we introduce ligand field theory.

