Question

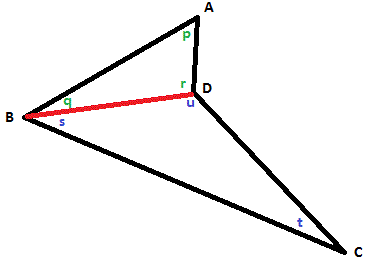
Why is the sum of angles in a quadrilateral equal to 360 degrees?

Answer 1

A quadrilateral can be divided with a diagonal into two triangles each with an interior angle sum of `180^@`

Explanation:

It really depends upon how far back you want to go for this proof.

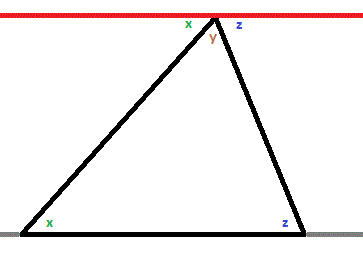
If you accept that the interior angles of a triangle add up to `180^@`

`"Interior angles of "triangle ABD = color(green)(p+q+r =180^@)`
`"Interior angles of "triangle DBC = color(blue)(u+s+t=180^@)`

`"Interior angles of "square ABCD = color(green)(p+q+r)+color(blue)(u+s+t)`
`color(white)("XXXXXXXXXXXXXXXXX")=color(green)(180^@)+color(blue)(180^@)`
`color(white)("XXXXXXXXXXXXXXXXX")=360^@`

If you need to prove that the interior angles of a triangle add up to `180^@`
you can use the rule that the interior angles on the opposite sides of a line crossing two parallel lines are equal.

`"Interior angles of " triangle = x+y+z`
`color(white)("XXXXXXXXXXXXX")= "Sum of angles in a straight line"`
`color(white)("XXXXXXXXXXXXX")= 180^@`