Question

You have found a fossilized leg bone of some unknown mammal. Based on the size of the bone, you determine that it should have contained about 100 g of carbon-14 when the animal was alive. The bone now contains 12.5 g of carbon-14. How old is the bone?

Answer 1

`"17,190 years"`

Explanation:

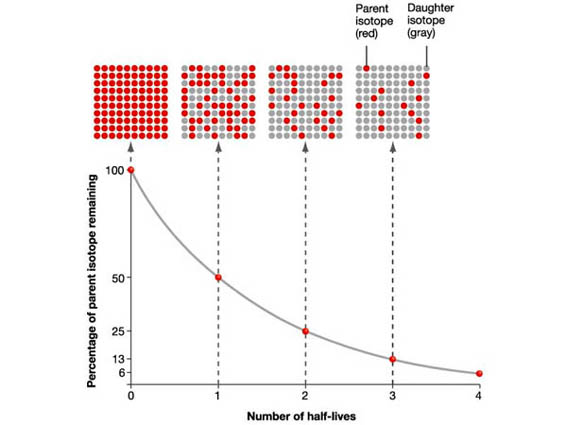
Nuclear half-life is simply a measure of how much time must pass in order for a sample of a radioactive substance to decrease to half of its initial value.

Simply put, in one nuclear half-life, half of the atoms in the initial sample undergo radioactive decay and the other half do not.

http://begoduqakuwa.net63.net/half-life-of-radioactivity-decay.php

Since the problem doesn't provide the nuclear half-life of carbon-14, you will have to do a quick search.

You'll find it listed as

`t_"1/2" = "5730 years"`

https://en.wikipedia.org/wiki/Carbon-14

So, what does that tell you?

An initial sample of carbon-14, `A_0`, will be halved with the passing of every half-life, which in your case is `5730` years. You can thus say that you'll be left with

`A_0 * 1/2 ->` after the passing of one half-life

`A_0/2 * 1/2 = A_0/4 ->` after the passing of two half-lives

`A_0/4 * 1/2 = A_0/8 ->` after the passing of three half-lives

`A_0/8 * 1/2 = A_0/16 ->` after the passing of four half-lives

`vdots`

and so on.

You can thus say that `A`, the mass of the radioactive substance that remains undecayed, will be equal to

`color(blue)(A = A_0 * 1/2^n)" "`, where

`n` - the number of half-lives that pass in a given period of time

So, you know that you start with `"100.0 g"` of carbon-14, and end up with `"12.5 g"` after the passing of an unknown amount of time.

This means that you can say

`overbrace(12.5 color(red)(cancel(color(black)("g"))))^(color(orange)("remaining mass")) = overbrace(100.0 color(red)(cancel(color(black)("g"))))^(color(purple)("initial mass")) * 1/2^n`

Rearrange to get

`12.5/100.0 = 1/2^n`

`1/8 = 1/2^n implies 2^n = 8`

Since `8 = 2^3`, you will have

`2^n = 2^3 implies n = 3`

So, three half-lives must pass in order for your sample of carbon-14 to be reduced from `"100.0 g"` to `"12.5 g"`. Since

`color(blue)(n = "period of time"/"half-life" = t/t_"1/2")`

you can say that

`t = n xx t_"1/2"`

In your case,

`t = 3 xx "5730 years" = color(green)("17,190 years")`

The answer should be rounded to three sig fig, but I'll leave it as-in, just for good measure.