Negative Exponents
Key Questions
-
I suppose you mean the fact that a number to the zero exponent is always equal to one, for example:
#3^0=1# The intuitive explanation can be found remembering that:
1) dividing two equal numbers gives 1;
ex.#4/4=1#
2) The fraction of two equal numbers a to the power of m and n gives:
#a^m/a^n=a^(m-n)# Now:
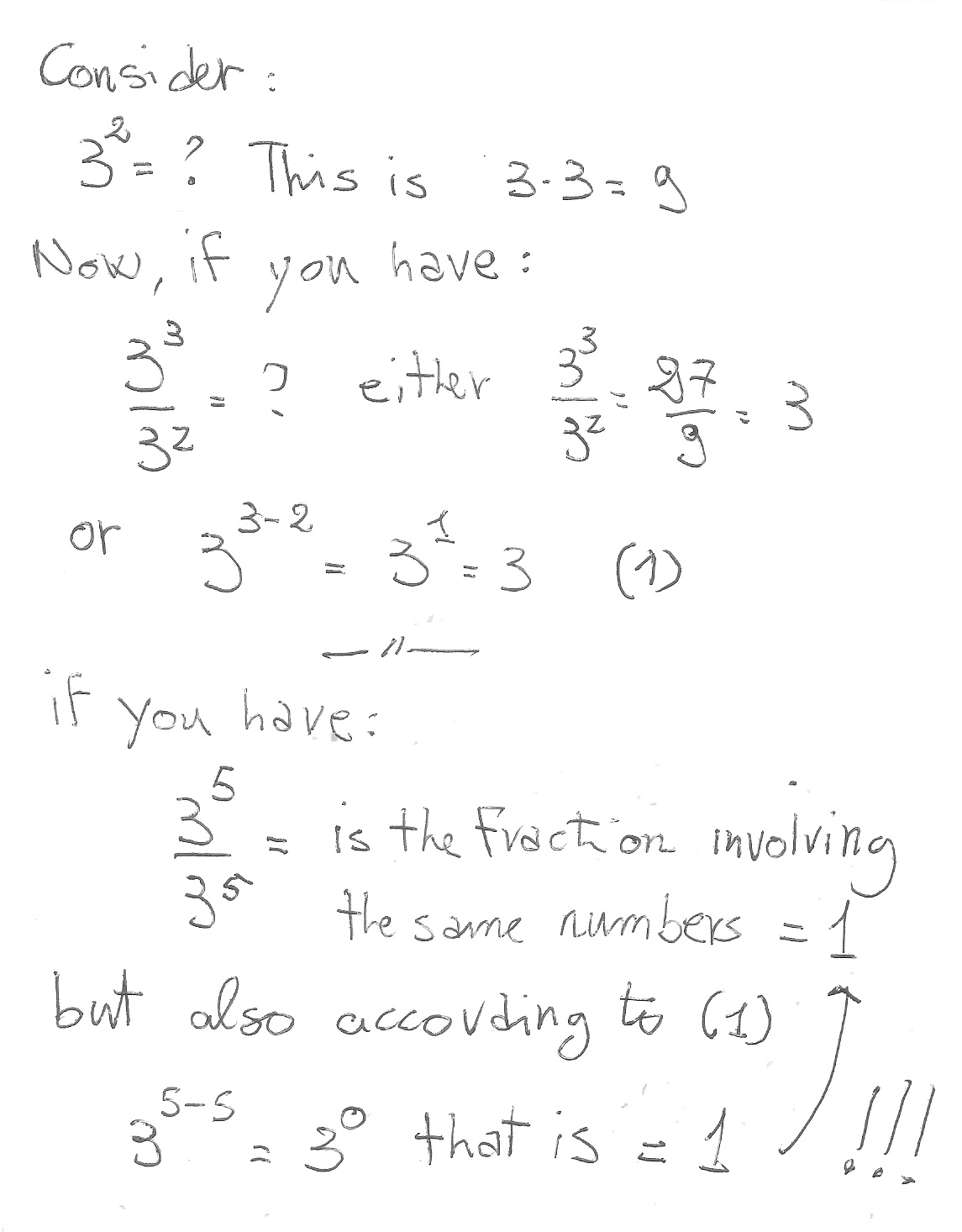
-
Negative exponents are an extension of the initial exponent concept.
To understand negative exponents ,
first review what we mean by positive (integer) exponentsWhat do we mean when we write something like:
#n^p# (for now, assume that#p# is a positive integer.One definition would be that
#n^p# is#1# multiplied by#n# ,#p# times.Note that using this definition
#n^0# is#1# multiplied by#n# ,#0# times
i.e.#n^0 = 1# (for any value of#n# )Suppose you know the value of
#n^p# for some particular values of#n# and#p#
but you would like to know the value of#n^q# for a value#q# less than#p# For example suppose you knew that
#2^10 = 1024# but you wanted to know what#2^9# was equal to.
Is there a faster way than multiplying#1# by#2# ,#9# times?
Yes.
If we note that#2^9 = (2^10)/2#
we can simply divide#1024# by#2# (giving 512) to obtain#2^9# In general if we know that the value of
#n^p# is#k#
and we want to know the value of#n^q# when#q<p#
we can simply divide k by n^(p-q)With this in mind what is the value of
#n^(-t)# ?
We know that#n^0 = 1#
so#n^(-t)# must be#1# divided by#n# ,#(0 - (-t))# timesThat is
#n^(-t) = 1/n^t# As a final example consider the descending powers of 3 in the following, noting that with each line down the result is decreased by dividing the current value by 3
#3^4 = 81#
#3^3 = 27#
#3^2 = 9#
#3^1 = 3#
#3^0 = 1#
#3^(-1) = 1/3#
#3^(-2) = 1/9#
#3^(-3) = 1/27# -
Raising to the -1 power is equivalent to taking the reciprocal, so we have
#(a/b)^{-1}=b/a#
I hope that this was helpful.
-
#x^(-n) = 1/(x^n)# Maybe you were asking for something more than this (???)
-
You can start by rewriting in the following way:
#b^{-x}=1/b^x#
I hope that this was helpful.
Questions
Exponents and Exponential Functions
-
Exponential Properties Involving Products
-
Exponential Properties Involving Quotients
-
Negative Exponents
-
Fractional Exponents
-
Scientific Notation
-
Scientific Notation with a Calculator
-
Exponential Growth
-
Exponential Decay
-
Geometric Sequences and Exponential Functions
-
Applications of Exponential Functions