Use Graphs to Solve Quadratic Equations

Key Questions

  • How do you find the zeros of a quadratic function?

    Take the whole function and set it equal to zero, then just solve it like you would a normal equation.

    LexiiRaee13 · 1 · Dec 15 2014
  • What do solutions to quadratic equations mean?

    Answer:

    A complex number '#alpha#' is called a solution or root of a quadratic equation #f(x) = ax^2 + bx + c #
    if #f(alpha) = aalpha^2 + balpha +c = 0#

    Explanation:

    If you have a function - #f(x) = ax^2 + bx + c #
    and have a complex number - #alpha# .

    If you substitute the value of #alpha# into #f(x)# and got the answer 'zero', then #alpha# is said to be the solution / root of the quadratic equation.

    There are two roots for a quadratic equation .

    Example :

    Let a quadratic equation be - #f(x) = x^2 - 8x + 15#

    The roots of it will be 3 and 5 .

    as #f(3) = 3^2 - 8*3 + 15 = 9 - 24 +15 = 0# and

    #f(5) = 5^2 - 8*5 + 15 = 25 - 40 +15 = 0# .

    Pradyun Devarakonda · 1 · May 22 2018
  • How do you use a graphing calculator to solve quadratic equations?

    Let us look at the following example.

    Solve #2x^2+5x-3=0# for #x#.

    (Be sure to move all terms to the left-hand side so that you have zero on the right-hand side.)

    Step 1: Go to "Y=" and type in the quadratic function.

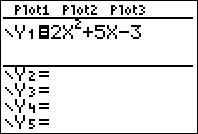
    enter image source here

    Step 2: Go to "WINDOW" to set an appropriate window size.

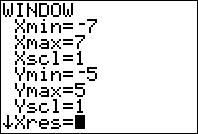
    enter image source here

    Step 3: Go to "CALC", and choose "zero".

    enter image source here

    Step 4: It will say "Left Bound?", so move the cursor to the left of the zero and press "ENTER".

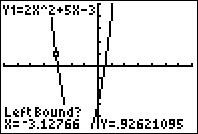
    enter image source here

    Step 5: It will say "Right Bound?", so move the cursor to the right of the zero and press "ENTER".

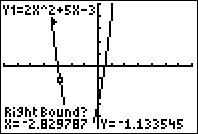
    enter image source here

    Step 6: It will say "Guess?", then move the cursor as close to the zero as possible and press "ENTER".

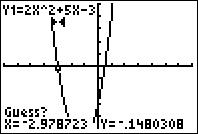
    enter image source here

    Step 7: The zero (#X=-3#) is displayed at the bottom of the screen.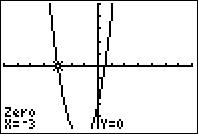

    enter image source here

    Step 8: Repeat Step 3-7 to find the other zero (#X=0.5#).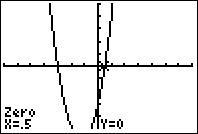

    enter image source here

    I hope that this was helpful.

    Wataru · 2 · Oct 30 2014
  • How do you use graphs to solve quadratic equations?

    If you are solving the quadratic equation of the form

    #ax^2+bx+c=0#,

    and the graph of the quadratic function #y=ax^2+bx+c# is available, then you can solve the quadratic equation by finding the x-intercepts (or zeros) of the quadratic function.

    I hope that this was helpful.

    Wataru · 2 · Oct 31 2014

Questions

Quadratic Equations and Functions