Question

How do I graph the quadratic equation `y=x^2+4x+6`?

Answer 1

You have a quadratic function in the form `y=ax^2+bx+c` which represents, graphically, a PARABOLA.
You can start by observing that the coefficient of the `x^2` is positive so that your parabola has an upward concavity, i.e., has a shape like a U.
Then you need to determine 3 sets of coordinates that characterize your parabola:
1) The Vertex: this is the lowest point of your parabola (the bottom of your U).
to find its coordinates (`x_v and y_v`) you use the fact that:
`x_v=-b/(2a)` and `y=-Delta/(4a)`

Where `Delta=b^2-4ac`

2) Crossing point with the `y` axis:
This point has coordinates: (`0, c`)

3) Crossing point(s) with the `x` axis:
These are obtained putting `y=0` and solving the corresponding second degree equation: `ax^2+bx+c=0`
If the equation doesn't have solutions (`Delta<0`) your parabola doesn't cross the `x` axis.
If `Delta=0` your vertex is also the point of crossing with the `x` axis.

In our case we have:

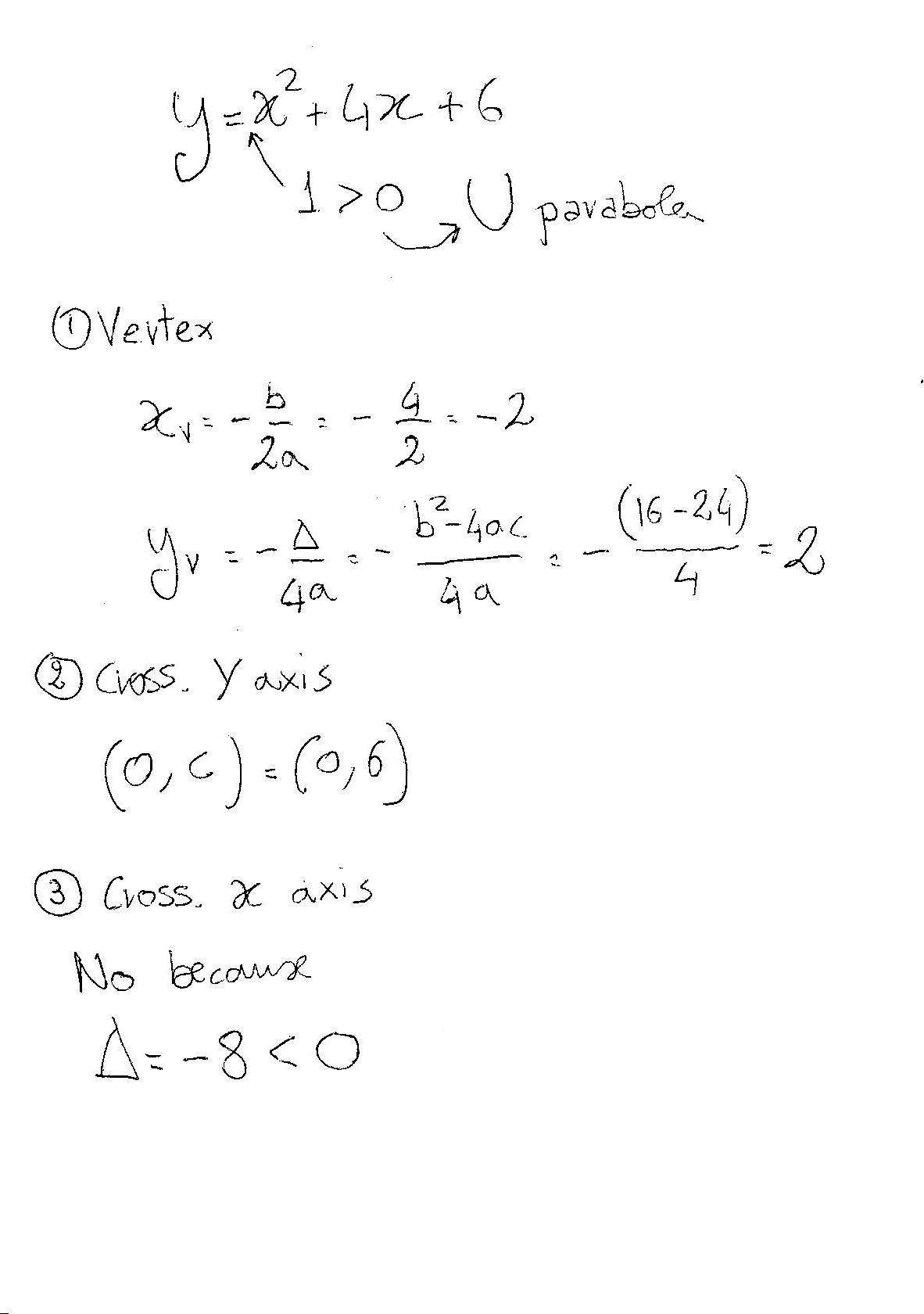
and: