If #1+3i# is a zero of #f#, what are all the zeros of #f(x)=x^4–3x^3+6x^2+2x-60#?
1 Answer
Apr 14, 2015
If
There are two ways:
-
Expand:
#(x-(1+3i))(x - (1-3i))# (factor theorem)
#x^2-(1+3i)x-(1-3i)x+10 = x^2 - 2x + 10# -
Use the sum and product of roots :
#1+3i+1 - 3i= 2# and#(1+3i)(1-3i)= 1 + 9 = 10# . Sum is equal to#-b/a# , so#-b/a=2/1# and#c/a=10/1# . One can solve to find a = 1, b = -2 and c = 10.
Now, for the long division :
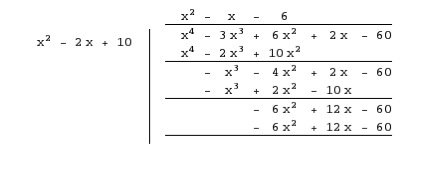
FINALLY, we can now factor

