Question

How do you solve a triangle if you are given a = 11, b = 14, c = 20?

Answer 1

Have a look (and check my math):

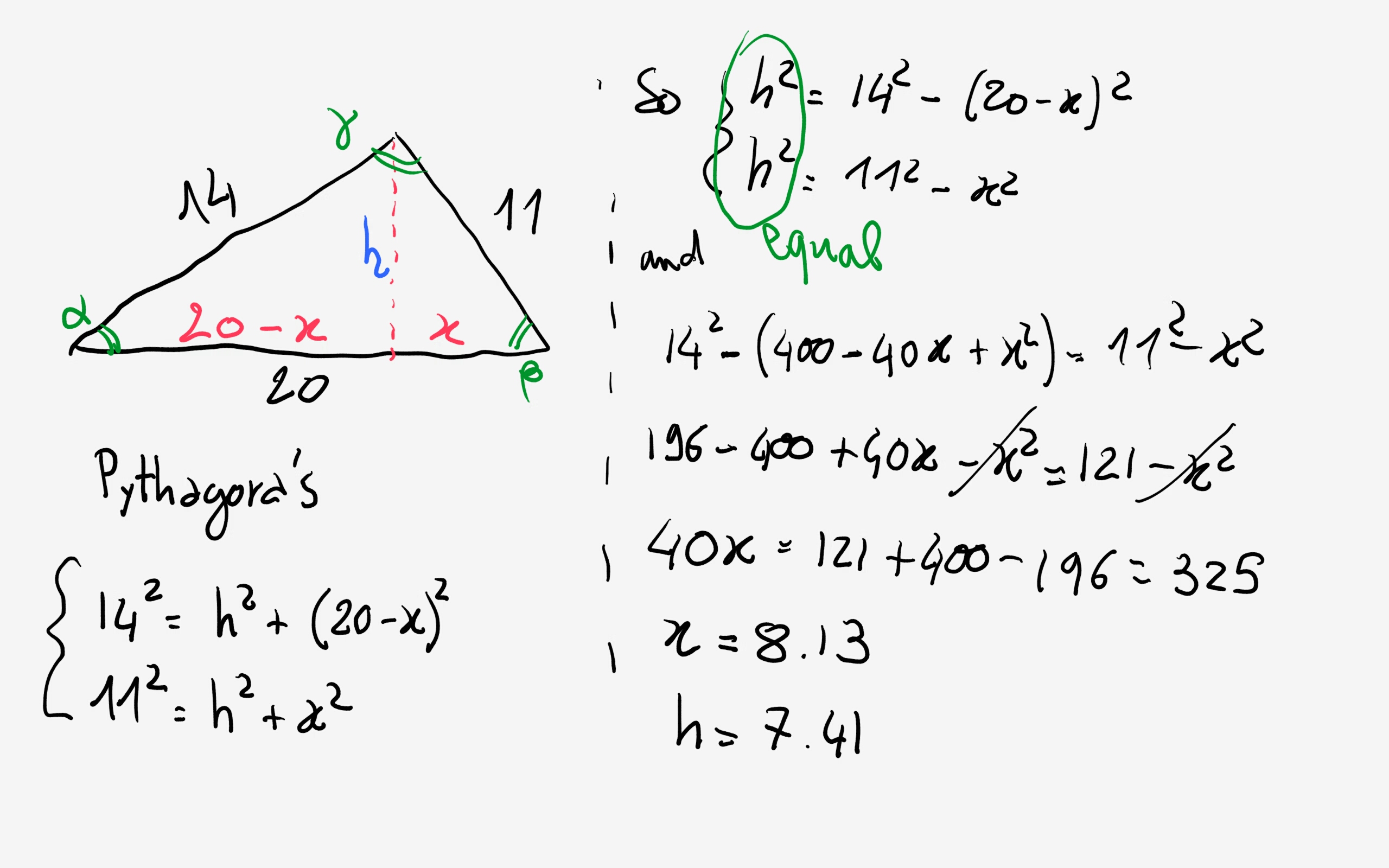
So:
`h=7.41=14sin(alpha)` then `alpha=31.95°`
`h=7.41=11sin(beta)` then `beta=42.35°`
`gamma=180-31.95-42.35=105.70°`

Answer 2

Use the trig identity: c^2 = a^2 + b^2 - 2ab.cosC

400 = 121 + 196 - 308.cos A

`cos A = -83/308 = - 0.27 -> A = 105.66`

Next, find cos B.

196 = 400 + 121 - 440.cos B

`cos B = 325/440 = 0.74 --> B = 42.38` deg

C = 180 - A - B = 180 - 105.66 - 42.38 = 31.96