Question

How do you use integrals to find the area bounded by the curve y = (x^2 - 9) and the x-axis for x = 0 to x = 5?

Answer 1

I found: area`=-10/3`

Explanation:

You write it as:
`int_0^5(x^2-9)dx=`
you can break it into two as:
`int_0^5(x^2)dx-int_0^5(9)dx=`
integrating you get:
`x^3/3-9x|_0^5`

now you use you extremes of integration substituting them and subtracting the resulting expressions as:
`(5^3/3-9*5)-(0^3/3-9*0)=`
`=125/3-45=-10/3`

You may wonder about the negative sign but looking at your area:

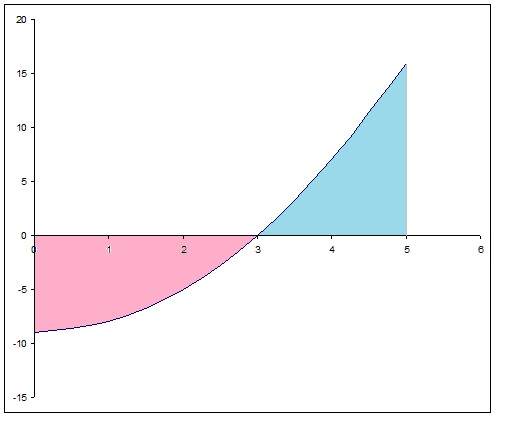
you can see that quite a big chunk (pink) is below the `x` axis giving a negative contribution (this are is equal to `-18`) while the blue part (positive) gives you a contribution of only `14.6`.