Question

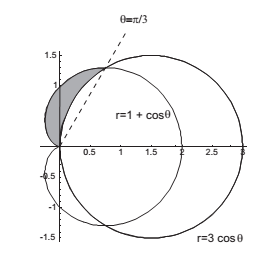
How do you find the region inside cardioid `r=1+cos(theta)` and outside the circle `r=3cos(theta)`?

Answer 1

It is `pi/4`

Explanation:

Find the intersection points of the curves hence we have that

`3cosθ=1+cosθ=>cosθ=1/2=>θ=+-pi/3`

The saded area is

(cardiod area from pi/3 to pi)-(cricle area from pi/3 to pi/2)

The cardiod area is

`int_(pi/3)^(pi) 1/2*(1+cosθ)^2dθ=pi/2-9/6*sqrt3`

and the circle area is

`int_(pi/3)^(pi/2) 1/2*(3*cosθ)^2dθ=(3pi/8)-9/16*sqrt3`

Hence the shaded area is `pi/8`

The total amount is `2pi/8=pi/4`

A graph for the curves is