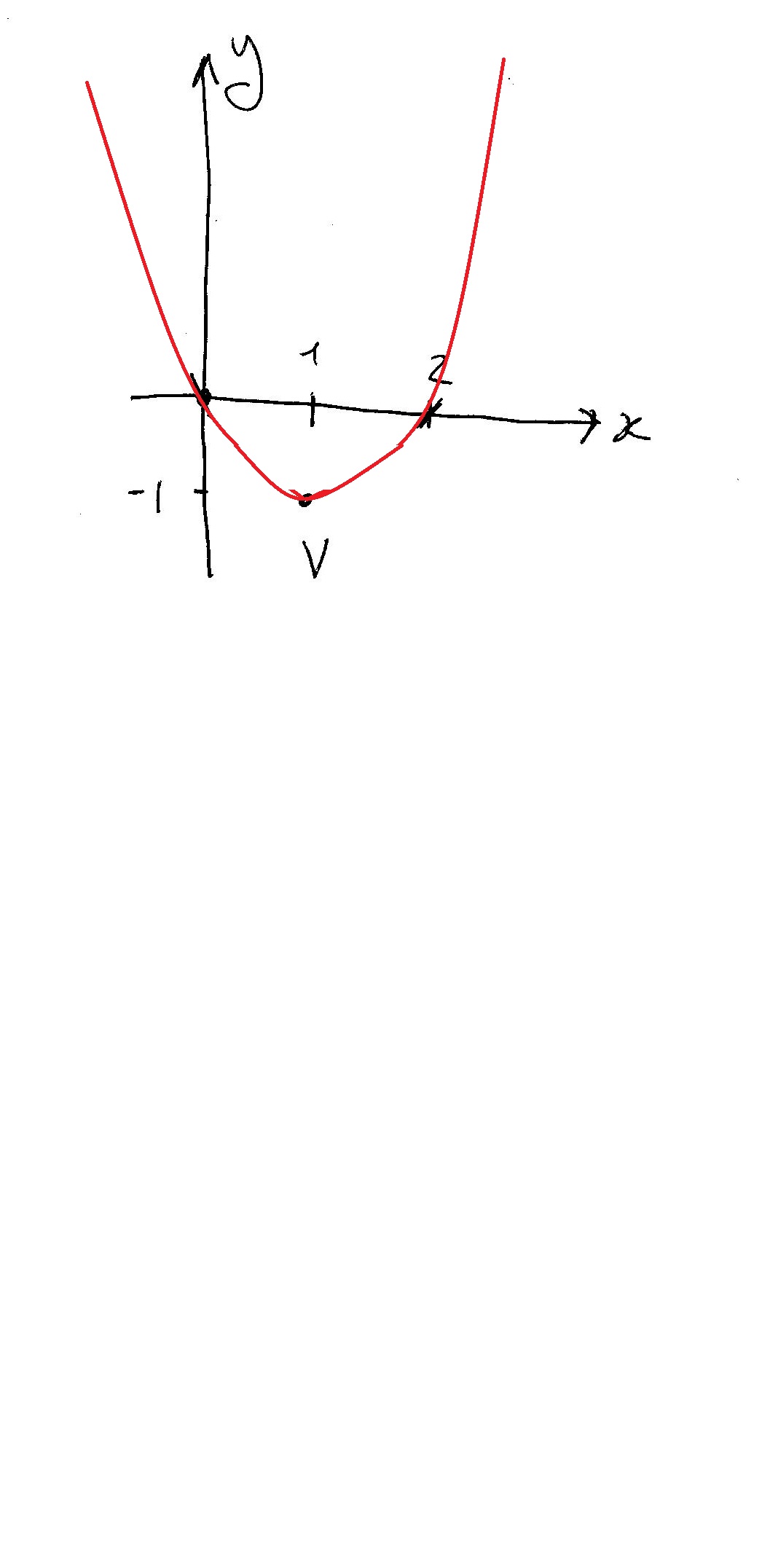
How do you identify the important parts of #y = x^2 – 2x# to graph it?
1 Answer
We can write your function in the general form:
Explanation:
Basically, to graph your function (that is a Quadratic, representing a Parabola) you need to observe:
1) the coefficient
If it is
2) the vertex: this is the highest/lowest point reached by your parabola and the parabola is plotted all around it. The coordinates of this special point are given as:
So vertex
3) y-intercept. You can set
4) x-intercept(s) (when they exist). You set
and:
So x-intercepts at
You can now plot your parabola using mainly these points: