Question

What is the formula for the area of a trapezoid?

Answer 1

In a trapezoid with bases `b_1` and `b_2` and height `h`, the area is given by `area = (b_1+b_2)/2h`

Explanation:

To derive the formula, let's consider the following trapezoid

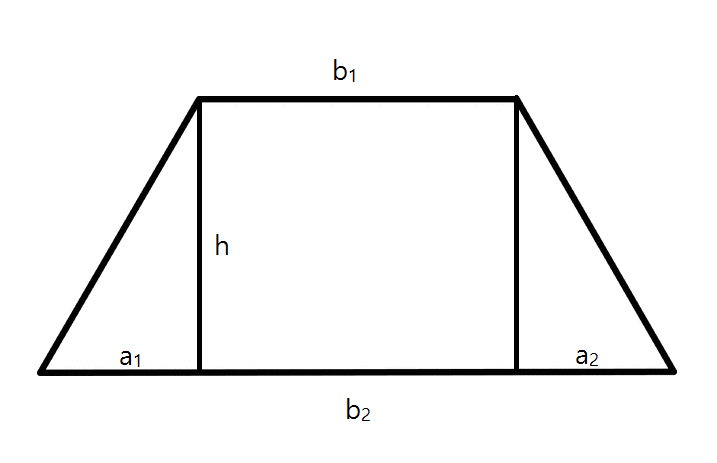
The area of the trapezoid is clearly the sum of the areas of the two triangles and the rectangle formed by the additional lines constructed.

The rectangle has sides of length `h` and `b_1` and thus has area `b_1h`

The triangles have areas `a_1/2h` and `a_2/2h` respectively, and so their sum is `(a_1 + a_2)/2h`

But
`a_1 + b_1 + a_2 = b_2`
`=> a_1 + a_2 = b_2 - b_1`

So the sum of the areas of the triangles is `(b_2-b_1)/2h`

Finally, we add that to the area of the rectangle to obtain the area of the trapezoid as

`area = b_1h + (b_2-b_1)/2h= (2b_1)/2h+(b_2-b_1)/2h =(2b_1 + b_2 - b_1)/2h`
`=> area =(b_1+b_2)/2h`