Question

What is the area of a parallelogram with corners at these coordinates on a plane: (-2,-1), (-12,-4), (9,-4), (-1,-7)?

Answer 1

Let see the figure which shows the parallelogram with given vertices

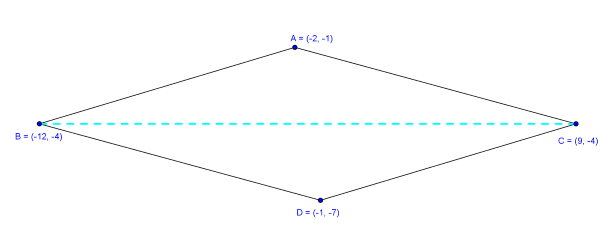
As the diagonal of a parallelogram BC divides into two congruent triangles, which implies the triangles have same area.

So, the area of the parallelogram will be 2 times the area of the triangle ABC.

We know from analytical geometry that the area of a triangle with given vertices is

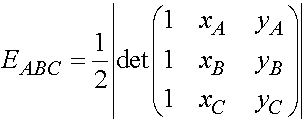
where `(x_A,y_A)` ,`(x_B,y_B)`,`(x_C,y_C)` are the coordinates of points A,B,C.

Now we just have to replace the values in the formula above and find the value for `E_(ABC)`

Hence the area of the parallelogram is

`E_(ABCD)=2*E_(ABC)`