Question

Where does the maximum electron density occur for 2s and 2p orbitals in hydrogen atom?

Answer 1

For hydrogen, we have to use spherical harmonics, so our dimensions are written as `(r, theta, phi)`. The wave function is defined as follows, via separation of variables:

`color(green)(psi_(nlm_l)(r,theta,phi) = R_(nl)(r) Y_(l)^(m_l)(theta, phi))`

`R_(nl)(r)` is the radial component of the wave function `psi_(nlm_l)(r,theta,phi)`, `Y_(l)^(m_l)(theta,phi)` is the angular component, `n` is the principal quantum number, `l` is the angular momentum quantum number, and `m_l` is the projection of the angular momentum quantum number (i.e. `0, pm l`). The wave function represents an orbital.

If you don't understand all of that, that's fine; it was just for context.

To get the maximum electron density, you have to look at probability density curves.

If we plot `4pir^2R_(nl)(r)^2` against `r`, we get the probability density curves for an atomic orbital.

The `2s` orbital's plot looks like this:

From this, you can tell that the maximum electron density occurs near `5a_0` (with `a_0 ~~ 5.29177xx10^(-11) "m"`, the Bohr radius) from the center of the atom, and `4pir^2 R_(20)(r)^2` is about `2.45` or so.

From this similar diagram, we can compare the `2s` with the `2p` orbital:

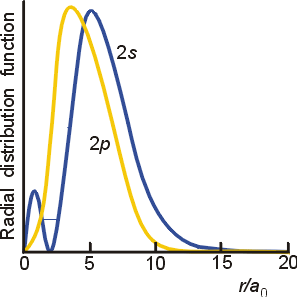
Here, you should see that the `2p` orbital has a maximum electron density near about `4a_0` from the center of the atom, and the value of `4pir^2 R_(21)(r)^2` is perhaps around `2.5`.

This should make more sense once you realize what the probability density plots of the `2s` and `2p` orbitals look like:

2s

2p

"The density of the [dark spots] is proportional to the probability of finding the electron in that region" (McQuarrie, Ch. 6-6).

Basically, start with a radius of 0, and expand your radius of vision outwards from the center of the orbital, and you should be constructing the probability density curves (radial distribution plots).