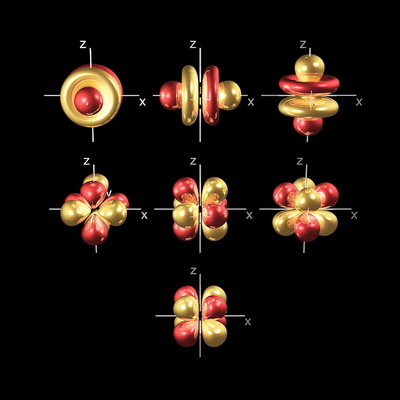The orbitals come from the quantum numbers needed to solve the Schrödinger equation.
The principal quantum number #n#, determines the energy of the orbital. Allowed values are #n = 1, 2, 3, 4, …#
The azimuthal quantum number #l#, determines the shape of the orbital. Allowed values are integers from #0 " to " n#.
#l = 3# corresponds to an #f# orbital.
The magnetic quantum number #m_l#, determines how many orbitals there are in the subshell. Allowed values are integers from #–l " to " +l#.
If #l = 3#, the allowed values of #m_l# are #"-3, -2, -1, 0, 1, 2, 3"#.
So there are seven #f# orbitals in a subshell.
Four of the #4f# orbitals look like eight-leafed clovers, and three look like #p# orbitals with two doughnuts around their middle.
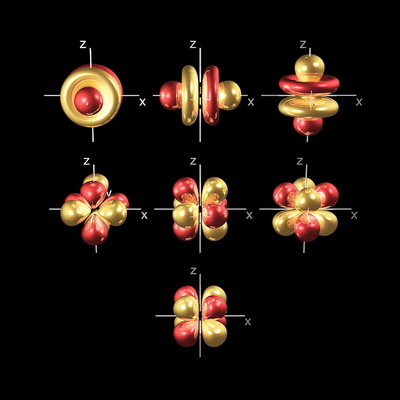
(from chemistry.caddell.org)