Question

An object with a mass of `4 kg` is on a plane with an incline of `- pi/8`. If it takes `18 N` to start pushing the object down the plane and `5 N` to keep pushing it, what are the coefficients of static and kinetic friction?

Answer 1

I found `0.91 and 0.55` (but check my maths!).

Explanation:

Have a look at the diagram:

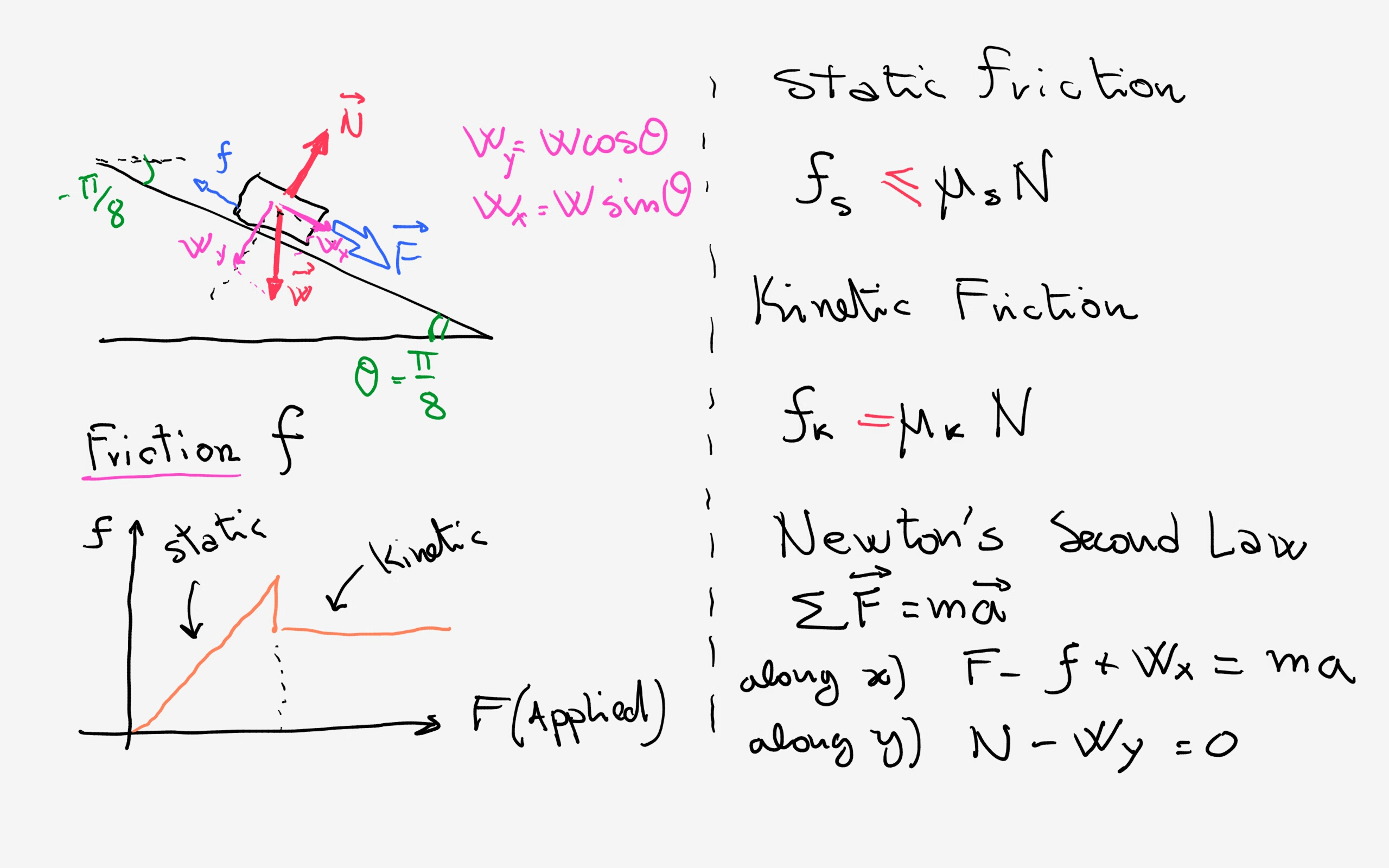
I assumed that the negative angle represents the downward inclination of the surface and transferred it as `theta` as in figure (I may be wrong though...).
With this convention for the angle and Newton's law:

`N=W_y=Wcos(theta)=mgcos(theta)=4*9.8*cos(pi/8)=36.2N`

Also: `W_x=Wsin(theta)=4*9.8*sin(pi/8)=15N`

Now:

1) Static Friction:
I consider the object still at rest but almost moving. Acceleration will be zero and we will be at maximum static friction where it will exactly be: `f_s=mu_sN`

So, we use Newton's law along `x` with `a=0` to get:

`F-f_s+W_x=0`
`color(red)(18)-(mu_s*36.2)+15=0`
`mu_s=0.91`

2) Kinetic Friction:
From our graph of friction we can see that Kinetic friction will be almost constant and so:
`f_k=mu_kN`

Here we can assume that the object will move with constant velocity down the incline giving again zero acceleration. As before we get, using Newton's law along `x` with `a=0`:

`F-f_k+W_x=0`
`color(red)(5)-(mu_k*36.2)+15=0`
`mu_k=0.55`