Question

A parallelogram has sides A, B, C, and D. Sides A and B have a length of `7` and sides C and D have a length of `6`. If the angle between sides A and C is `(3 pi)/8`, what is the area of the parallelogram?

Answer 1

`38.803 " square units"`

Explanation:

Refer to the figure below

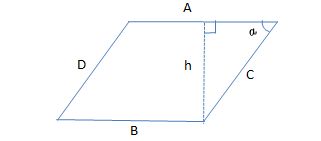
A and B are the parallel sides with the same length, 7. C and D are also parallel sides with the same length, 6. `alpha=(3pi)/8 radians=67.5^@.`

Side C meets side A, forming angle alpha. If we draw a line from the other endpoint of side C, a line that is perpendicular to side A, the obtained segment is the height (`"h"`) relatively to side A. As we can see from the figure:
`sin alpha="opposed cathetus"/"hypotenuse"`
`sin 67.5^@=h/C` => `h=6*sin 67.5^@~=5.543`

Since the area of a parallelogram is given by
`A=base xx height`
`A=7*6*sin 67.5^@~=38.803`