Question

What is the focus of the parabola `y=1/8(x^2−4x−12)`?

Answer 1

`(2,0)`

Explanation:

Complete the square.

`y = (x-2)^2/8 -2`

From the symmetry, we know that the focus lies on the line `x=2`.

Now, you can use the formula if you have memorized it. But I am going to work it out physically.

If you know a special property of parabola (or paraboloid) mirrors, is that any ray that comes parallel to the symmetric axis, after the reflection, will pass through the focus.

We have already found the `x` coordinate of the focus. Now, according to the law of reflections, the angle of incidence equals to the angle of reflection. If a ray comes down vertically and strikes a surface with gradient of 1, it will be reflected horizontally.

Here is an illustration.

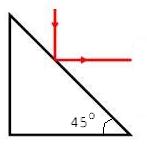
Therefore, we have to find a point with `frac{dy}{dx} = +-1`.

We differentiate to get

`frac{dy}{dx} = frac{x-2}{4}`

When `frac{dy}{dx} = 1`, `x = 6`.

When `x = 6`, `y = 4`

So we know now that the `y` coordinate of the focus is 4.