How do you find the axis of symmetry, graph and find the maximum or minimum value of the function f(x) = 2x^2 - 4x +1f(x)=2x2−4x+1?
2 Answers
To find the vertex and the axis of symmetry, rearrange the equation into vertex form by completing the square.
Explanation:
This equation is for a parabola, because it follows the general form
Hence the maximum or minimum value is at the vertex. In this case, because the squared term is positive, it will be a minimum value.
To find the vertex and the axis of symmetry, rearrange the equation into vertex form by completing the square.
This expression is at its minimum when
The axis of symmetry is
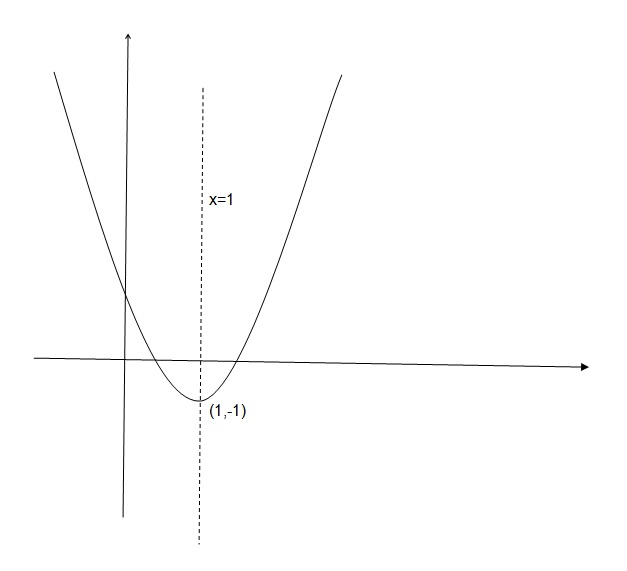 Sketch
Sketch
A slightly 'cheating' sort of way to find that the axis of symmetry is at
Explanation:
Given:
Write as
Now consider the
Apply:
Now compare this to the graph
 Tony B
Tony B


