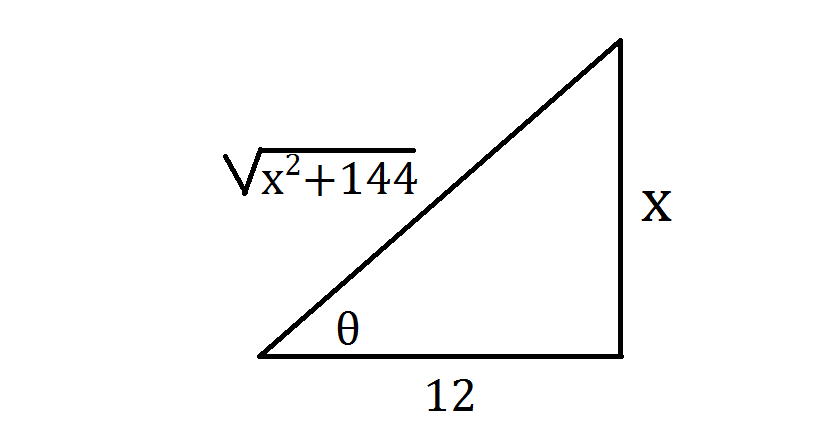Step 1: Draw It!
The first thing to do with trig substitution problems, especially if you have time, is to draw them out. Note that the expression in the denominator - #sqrt(144+x^2)# - resembles the Pythagorean Theorem, which says for any right triangle, the hypotenuse is #sqrt(a^2+b^2)#. We could rewrite #sqrt(144+x^2)# as #sqrt((12)^2+x^2)#, which looks pretty much the same as the theorem, with #a = 12# and #b = x#. Using this info, we can make a pretty picture of this problem:
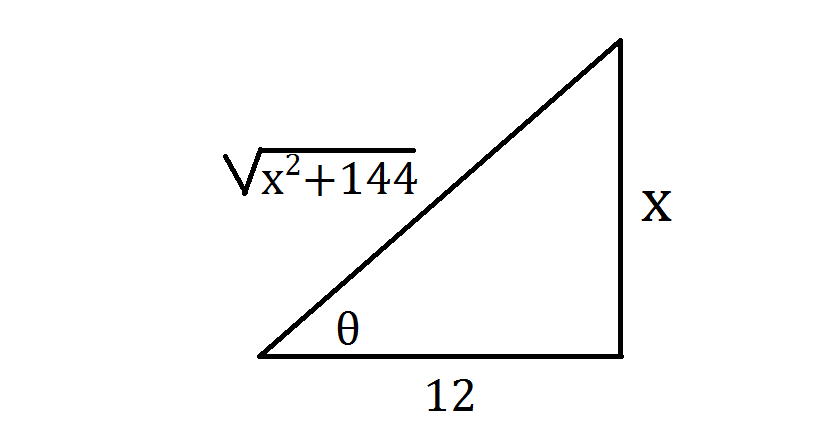
Step 2: Define a Few Things
From the image, we see that #tan(theta) = x/12# and furthermore, #12tan(theta) = x#. Taking the derivative of both sides, we see that #(dx)/(d theta) = 12sec^2(theta)#. Multiplying both sides by #d theta# yields #dx = 12sec^2(theta)d theta#.
Step 3: Trigonometric Substitution
Now we can finally take this information and apply it to the problem. Making substitutions, our integral becomes:
#int (12tan(theta))/(sqrt(144+(12tan(theta))^2)) 12sec^2(theta)d theta#
Step 4: Simplification
This tends to be pretty long, so bear with me here.
#=144int (tan(theta)sec^2(theta))/(sqrt(144+144tan^2(theta))) d theta#
#=144int (tan(theta)sec^2(theta))/(sqrt(144(1+tan^2(theta)))) d theta#
#=144int (tan(theta)sec^2(theta))/(12sqrt(1+tan^2(theta))) d theta#
#=12int (tan(theta)sec^2(theta))/(sqrt(1+tan^2(theta))) d theta#
Remember the Pythagorean Identities from trig? One of those identities is #1+tan^2(theta) = sec^2(theta)#. Using that fact,
#=12int (tan(theta)sec^2(theta))/(sqrt(sec^2(theta))) d theta#
#=12int (tan(theta)sec^2(theta))/(sec(theta)) d theta#
#=12int tan(theta)sec(theta)d theta#
Hm...think about it for a moment. What function's derivative is #tan(theta)sec(theta)#? Secant, of course! Which means our integral is...
#12sec(theta)+C#.
You might think we're done, but wait a minute. The problem was given to us in terms of #x#; our answer is in terms of #theta#. That leads us to...
Step 5: Reverse Substitution
Wonder why I told you to draw the problem? Because now we can clearly see from the triangle above that #sec(theta) = sqrt(144+x^2)/12#. Lastly, we deal with that pesky #12# in front of secant. Note that multiplying #12# to both sides of #sec(theta) = sqrt(144+x^2)/12# gives us #12sec(theta) = sqrt(144+x^2)#. Now that our answer is in terms of #x#, we can officially say we're done.
Final answer: #int x/sqrt(144+x^2) dx = sqrt(144+x^2)+C#