Question

What is the atomic number of the yet undiscovered element in which the 8s and 8p electron energy levels fill?

Answer 1

If you notice the pattern on the last element on each period, you should see that the number of elements per period goes as the number of quantum numbers allowed for that period (`2,8,8,18,18,32,32, . . .`).

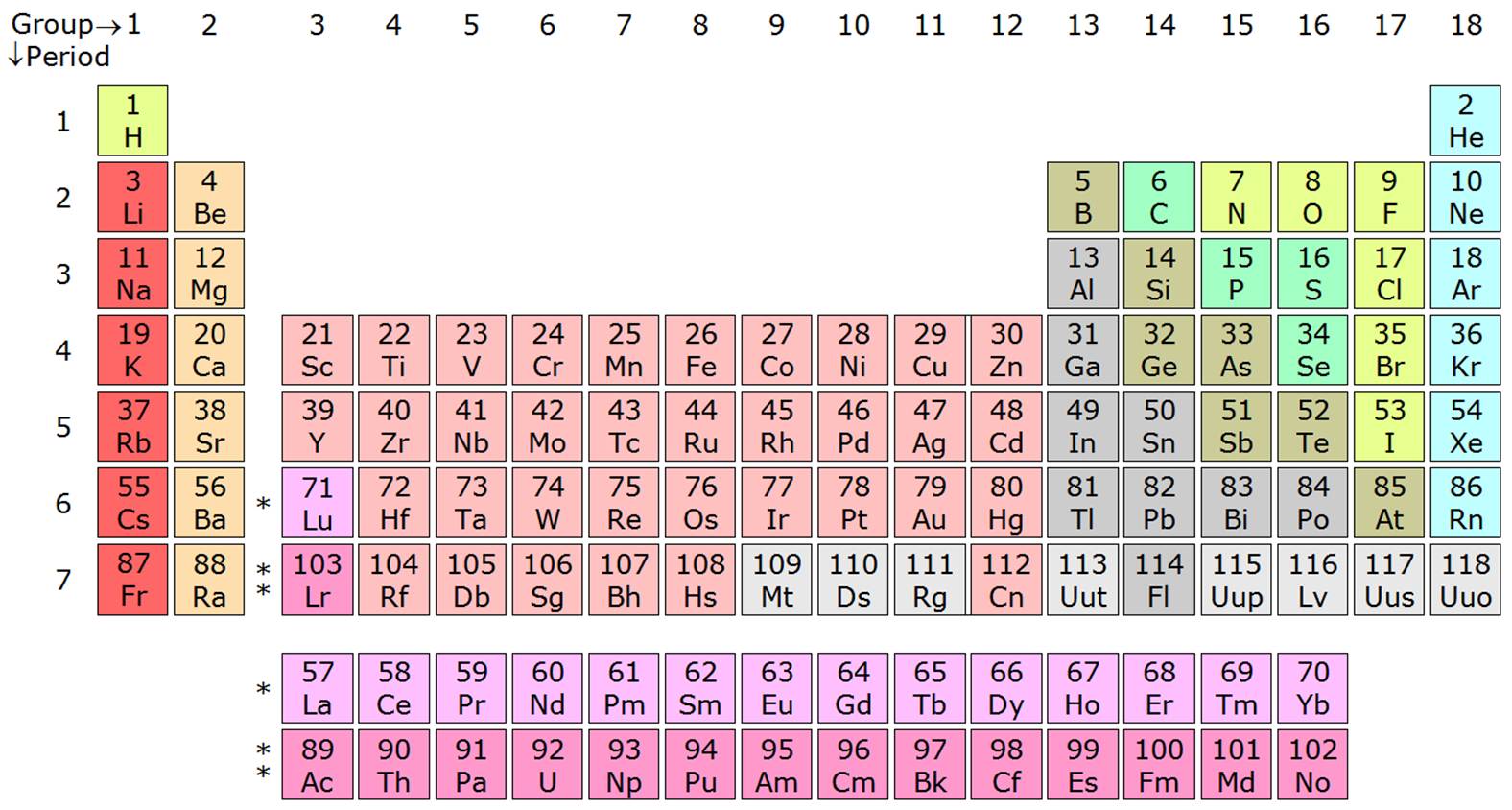
In other words:

• `0 + color(green)(2) = 2`
• `2 + color(green)(8) = 10`
• `10 + color(green)(8) = 18`
• `18 + color(green)(18) = 36`
• `36 + color(green)(18) = 54`
• `54 + color(green)(32) = 86`
• `86 + color(green)(32) = 118`
• `118 + color(green)(?) = "answer"`

So we need to determine the total number of quantum numbers `N_(m_l) xx N_(m_s)` allowed for `n = 8`, where `N_x` is the total number of `m_l` or `m_s`. Then, adding that to `118` gives us our answer.

Refer to this answer for a review of the quantum numbers.

1. If `n = 8`, then `l` takes on values in the set `{0, 1, . . . , n-1} = {0, 1, . . . , 7}`. For these values of `l`, we have the corresponding orbital types: `s, p, d, f, g, h, i, j`, for `l = 0,1,2,3,4,5,6,7`, respectively. But we only need up to `g`.
2. Therefore, `m_l` takes on values in the set `{0, pm1, . . . , pm7}`.
3. `m_s = pm"1/2"`.

Assuming the `g` orbitals (but not the `h` orbitals) come into play after ununoctium (`Z = 118`), we have the `8s`, `8p`, `7d`, `6f`, and `5g` orbitals to consider---following the pattern of `ns`, `np`, `(n-1)d`, `(n-2)f`, we should get `(n-3)g`.

• For the `8s`, `m_l = 0` and `m_s = pm"1/2"`.
• For the `8p`, `m_l = 0, pm1` and `m_s = pm"1/2"`.
• For the `7d`, `m_l = 0, pm1, pm2` and `m_s = pm"1/2"`.
• For the `6f`, `m_l = 0, pm1, pm2, pm3` and `m_s = pm"1/2"`.
• For the `5g`, `m_l = 0, pm1, pm2, pm3, pm4` and `m_s = pm"1/2"`.

So overall, we have `N_(m_l) xx N_(m_s) = (2l+1)*2` for all these to be:

`stackrel(8s)overbrace(1*2) + stackrel(8p)overbrace(3*2) + stackrel(7d)overbrace(5*2) + stackrel(6f)overbrace(7*2) + stackrel(5g)overbrace(9*2)`

`= 2 + 6 + 10 + 14 + 18 = color(green)(50)`.

Therefore, the element right below ununoctium should be `Z = 118+50 = color(blue)(168)`.