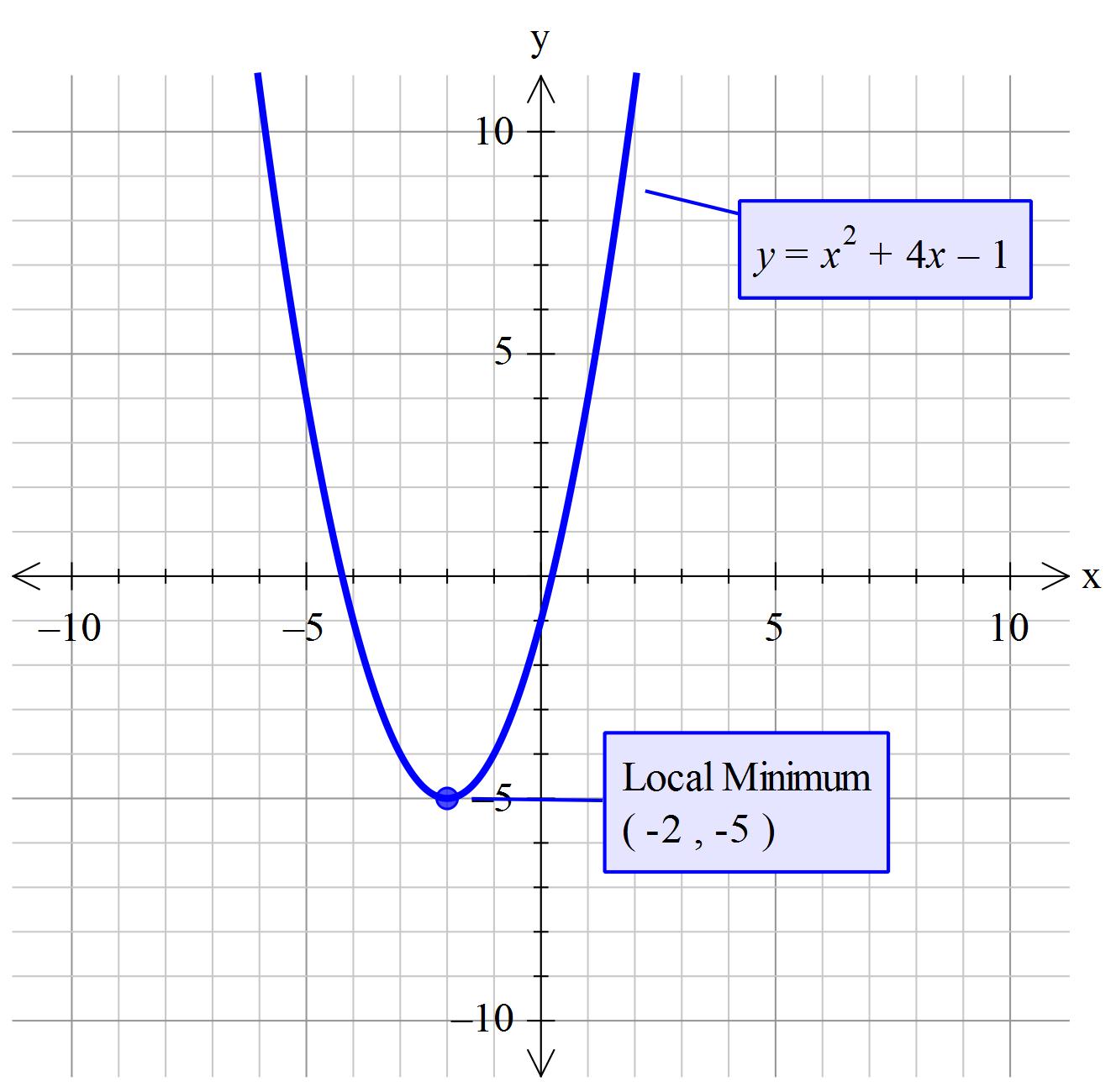
How do you find the axis of symmetry, graph and find the maximum or minimum value of the function #y = x^2 + 4x -1#?
1 Answer
Minimum at
Explanation:
The standard form is
This can be written as:
The axis of symmetry as at
This is also the value of
'.................................................................
Substitute for
'..........................................
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The coefficient of
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~