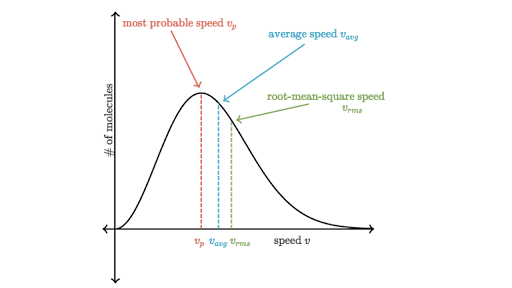
Why is most-probable speed correspond to the top of the Maxwell-Boltzmann distribution curve, even though the root-mean-square speed is the highest? Why are average and root-mean-square to the right?
1 Answer
Because most-probable speed is most likely, i.e. a greater fraction of molecules will have that speed. It does NOT indicate that it is the highest in magnitude---only likelihood.
Let
#upsilon_"mp" = sqrt((2k_BT)/m)# #<< upsilon >> = sqrt((8k_BT)/(pim))# #upsilon_"rms" = sqrt((3k_BT)/m)#
From factoring out everything that is not
The height on the y-axis does not indicate a faster speed.
I derive these equations below using the Maxwell-Boltzmann distribution (you would need to know how to perform derivatives, but the integrals used are tabled).
MOST PROBABLE SPEED
Given that
The
The Maxwell-Boltzmann speed distribution function (Physical Chemistry: A Molecular Approach, McQuarrie) is given as
#\mathbf(f(upsilon)dupsilon = 4pi(m/(2pik_BT))^"3/2" upsilon^2 e^(-m upsilon^2"/"2k_BT)dupsilon)# where
#k_B# is the Boltzmann constant,#T # is temperature,#m# is the mass of the gas, and#upsilon# is speed.
Taking the derivative with respect to
#color(green)((df(upsilon))/(dupsilon))#
#= color(green)(4pi(m/(2pik_BT))^"3/2" d/(dupsilon)[upsilon^2e^(-m upsilon^2"/"2k_BT)])#
Using the product rule, we have
#= 4pi(m/(2pik_BT))^"3/2" [upsilon^2cdot(-cancel(2)upsilon*m/(cancel(2)k_BT))e^(-m upsilon^2"/"2k_BT) + 2upsilone^(-m upsilon^2"/"2k_BT)]# where
#g(upsilon) = upsilon^2# ,#h(upsilon) = e^(-m upsilon^2"/"2k_BT)# , and#k(upsilon) = -(m upsilon^2)/(2k_BT)# .
Now simply note that the constants can never be
#= cancel(4pi(m/(2pik_BT))^"3/2") [e^(-m upsilon^2"/"2k_BT)(2upsilon - upsilon^3(m/(k_BT)))] = 0#
#= e^(-m upsilon^2"/"2k_BT)[2upsilon - upsilon^3(m/(k_BT))] = 0#
Of course,
#0 = 2upsilon - upsilon^3(m/(k_BT))#
So we get, given that speeds are always positive:
#upsilon^(cancel(3)^(2)) (m/(k_BT)) = 2cancel(upsilon)#
#upsilon^2 = (2k_BT)/(m) => color(blue)(upsilon_"mp") = color(blue)(sqrt((2k_BT)/m))#
AVERAGE SPEED
The average speed can be gotten from the integral formula for averages, using the Maxwell-Boltzmann distribution from before:
#color(green)(<< upsilon >> = int_(0)^(oo) upsilonf(upsilon)dupsilon)#
#= 4pi(m/(2pik_BT))^"3/2" int_(0)^(oo) upsilon^3 e^(-m upsilon^2"/"2k_BT)#
Using this tabled integral:
#int_(0)^(oo) x^(2n+1)e^(-alphax^2)dx = (n!)/(2alpha^(n+1))#
we utilize
#= 4pi(m/(2pik_BT))^"3/2" cdot 1/(2(m/(2k_BT))^(1+1))#
#= 4pi(m/(2pik_BT))^"3/2" cdot (2(k_BT)^2)/(m^2)#
#= 8pi(cancel(m)/(2pi))^"3/2"cancel((1/(k_BT))^"3/2") cdot ((k_BT)^(cancel("4/2")^"1/2"))/(m^(cancel("4/2")^"1/2"))#
#= 8pi(1/(2pi))^"2/2"cdot(1/(2pi))^"1/2" cdot ((k_BT)/(m))^"1/2"#
#= 4cdot ((k_BT)/(2pim))^"1/2"#
#=> color(blue)(<< upsilon >> = sqrt((8k_BT)/(pim)))#
ROOT-MEAN-SQUARE SPEED
Now, for the root-mean-square speed!
By definition,
#color(green)(<< upsilon^2 >> = int_(0)^(oo) upsilon^2f(upsilon)dupsilon)#
(You may want to compare this back to the average speed integral to see the difference.)
#= 4pi(m/(2pik_BT))^"3/2" int_(0)^(oo) upsilon^4 e^(-m upsilon^2"/"2k_BT)#
We use another tabled integral, since
#int_(0)^(oo) x^(2n)e^(-alphax^2)dx = (1cdot3cdot5cdots(2n-1))/(2^(n+1)alpha^n)(pi/(alpha))^"1/2"#
For this,
#=> 4pi(m/(2pik_BT))^"3/2"[(1cdot(2*2-1))/(2^(2+1)(m/(2k_BT))^2)(pi/(m/(2k_BT)))^"1/2"]#
#= 4pi(m/(2pik_BT))^"3/2"[(3)/(8(m/(2k_BT))^2)(pi/(m/(2k_BT)))^"1/2"]#
#= 4pi(m/(2pik_BT))^cancel("3/2")[(3/8) * ((2k_BT)/m)^2cancel(((2pik_BT)/m)^"1/2")]#
#= 3/cancel(2)(cancel(pi)m)/(cancel(2)cancel(pi)k_BT) ((cancel(2)k_BT)/m)^2#
#= 3cancel((m)/(k_BT)) ((k_BT)/m)^cancel(2)#
#= (3k_BT)/m#
Therefore:
#color(blue)(upsilon_"rms") = sqrt(<< upsilon^2 >>) = color(blue)(sqrt((3k_BT)/m))#
NOW WHAT?
Now why the heck did we do all that? To get the comparable formulas, of course! We have:
#upsilon_"mp" = sqrt((2k_BT)/m)# #<< upsilon >> = sqrt((8k_BT)/(pim))# #upsilon_"rms" = sqrt((3k_BT)/m)#
Notice that you can factor these out to get the following magnitude orders:
#sqrt3sqrt((k_BT)/m) > 2sqrt(2/pi)sqrt((k_BT)/(m)) > sqrt2*sqrt((k_BT)/m)#
That is,
As your Maxwell-Boltzmann distribution plot shows, the root-mean square speed is farthest to the right on the graph, meaning that it is largest, and the most-probable speed is farthest to the left, meaning that it is smallest, as predicted in the comparison above.

