How do you find the exact value of cos 7pi/4?
3 Answers
Explanation:
Evaluate
So
Now divide
That means
First, convert to degrees (for many people, these are more convenient to work with).
Explanation:
The conversion factor between radians and degrees is
Now, this is a special angle, which can be found by using the special triangles.
But first, we must determine the reference angle of
We now know that we must use the
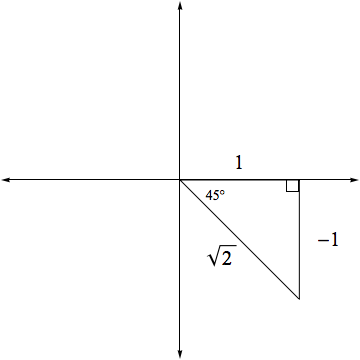 http://www.shmoop.com/trig-functions/special-trig-angle-obtuse.html
http://www.shmoop.com/trig-functions/special-trig-angle-obtuse.html
Now, it's just a matter of applying the definition of cos to find the wanted trig ratio.
Hopefully this helps!
Explanation:
Trig unit circle and trig table -->



