Question

What is the slope of a line perpendicular to the line whose equation is `3x-7y+14=0`?

Answer 1

Slope of the perpendicular line `-7/3`

Explanation:

`7y = 3x+14 or y= 3/7*x+2` So slope of the line `m_1=3/7` Hence slope of the perpendicular line `m_2=-1/(3/7) =-7/3` [Ans]

Answer 2

Put the original line in slope-intercept form, then take the negative reciprocal of the slope to find: `m_p = -7//3`

Explanation:

The slope of a perpendicular line, `m_p` to a line of slope `m` is given by

`m_p=-1/m`

This is straight forward to show graphically, which I'll do at the end of this answer. To find the perpendicular slope, we need to find the slope of the original line. The simplest way to do this is to put our original equation into slope-intercept format which is:

`y=mx+b`

Taking our equation, we need to isolate the term containing `y` on one side of the equation. We can do this by adding `7y` to both sides

`3x-7y+14+7y=0+7y`

Completing this step we get (where we can write the two sides of the equation in the opposite order - i.e. change right for left)

`7y=3x+14`

Now we can divide both sides by `7` to get

`y=3/7x+2`

Therefore the slope of our original line is

`m=3/7`

Using the equation for the perpendicular slope, we get:

`m_p = -1/m = -7/3`

Slope of normal line explanation:

If we have a line with slope `m` as shown by the blue line in the following graph:

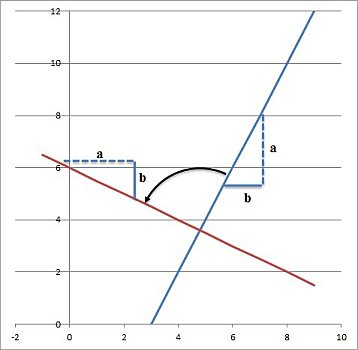
the slope can be calculated from the rise `a` and run `b` as

`m=a/b`

When we want to find the slope of a perpendicular (or normal) line, we need to rotate our line by 90 degrees. When we do this, we can keep the same construction for the rise and run attached to the new line shown in red. From the graph, we can see that the rise and run have now switched places, and the the sign of the rise has changed. So the new slope of the perpendicular line can be written:

`m_p=(-b)/a = - b/a`

We can now use the original slope in this equation by noting that we have the reciprocal in the new expression, such that

`m_p=-1/m`