Question

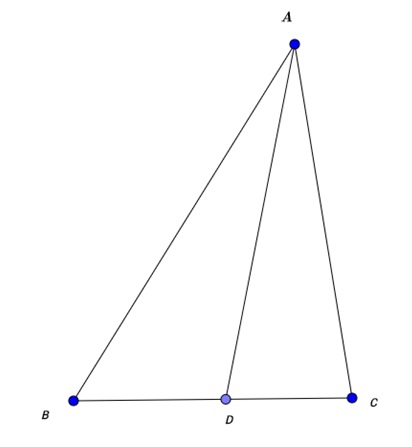
A triangle has corners points A, B, and C. Side AB has a length of `12`. The distance between the intersection of point A's angle bisector with side BC and point B is `4`. If side AC has a length of `10`, what is the length of side BC?

Answer 1

`BC=7.333`

Explanation:

According to angle bisector theorem, in a `DeltaABC`, if angle `A` is bisected and it cuts `BC` at `D`, then

`(AB)/(AC)=(BD)/(DC)`

As `AB=12`, `AC=10` and distance between the intersection of point A's angle bisector with side BC and point B i.e. `BD` is `4`,

we have `12/10=4/(DC)`

or `DC=(10xx4)/12=(10xxcancel4)/(3cancel12)=10/3=3.333`

Hence `BC=4+3.333=7.333`